可视化主流排序算法

2017年12月23日

目录

1 冒泡排序(Bubble Sort)

算法描述

  • 假设要从小到大进行排序
  • 对于一个元素可比较的序列，从始元素开始，依次比较与之相邻的元素，如果大于后者，则二者位置互换
  • 第一次遍历整个序列，最大的元素一定会移动到序列尾
  • 第二次遍历整个序列(不包括序列尾元素)，倒数第二大的元素会移动到序列倒数第二的位置
  • .
  • 遍历n-1次之后，整个序列排序完毕

算法动画演示

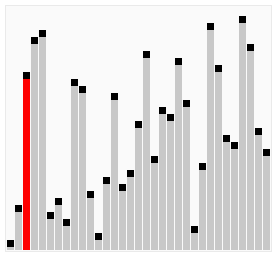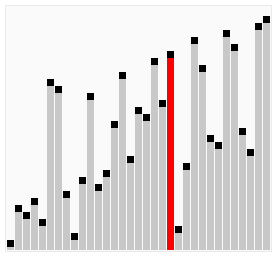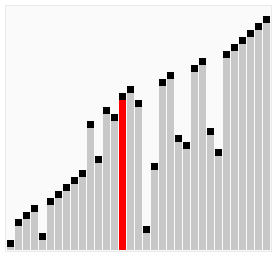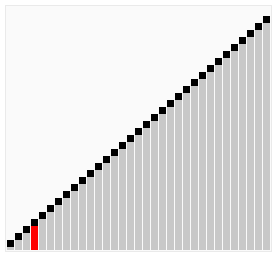
Sortinig bubble sort animation

算法实现(Java)

BubbleSort.java

import java.util.Random ;

public class BubbleSort{

    /*
     * This algorithm is not optimal, because we compare the element which has already ordered
     * when the sequence is ordered, it terminate. We know this from the boolean sorted
     */
    static void bubbleSort(int[] array){
        boolean sorted = false ;
        while(sorted = !sorted){
            for(int i=0; i<array.length-1; i++){
                if(array[i] > array[i+1]){
                    swap(array, i, i+1) ;
                    sorted = false ;
                }
            }
        }
    }

    /*
     * This algorithm for bubble sort is optimal, because we will not compare the element which has already ordered
     * The abrove method also can be revised by assign a new variable hi=array.length then hi --
     */
    static void bubbleSortRevised(int[] array, int lo, int hi){
        boolean sored = false ;
        while(sorted = !sorted){
            for(int i=lo; i<hi-1; i++){
                if(array[i] > array[i+1]){
                    swap(array, i, i+1) ;
                    sorted = false ;
                }
            }
            hi -- ;
        }
    }

    /*
     * This is the revised version for method bubbleSort()
     */
    static void bubbleSort2(int[] array){
        boolean sorted = false ;
        int hi = array.length ;
        while(sorted = !sorted){
            for(int i=0; i<hi-1; i++){
                if(array[i] > array[i+1]){
                    swap(array, i, i+1) ;
                    sorted = false ;
                }
            }
            hi -- ;
        }
    }

    static void swap(int[] array, int first, int last){
        int temp = array[first] ;
        array[first] = array[last] ;
        array[last] = temp ;
    }

    public static void main(String args[]){
        Random rnd = new Random(26) ;
        int[] array = new int[10] ;
        for(int i=0; i<array.length; i++){
            array[i] = rnd.nextInt(10) ;
        }
        bubbleSort(array) ;
        //bubbleSortRevised(array, 0, array.length) ;
        for(int i : array)
            System.out.print(i + "\t") ;
    }

}

复杂度分析

The best average worse case for bubble sort is in O(n^2)

2 选择排序(Selection Sort)

算法描述

  • 共要进行n-1次selection遍历
  • 每次遍历选择最小的元素，和起始遍历位置的元素进行互换
  • 每一次遍历后最小的元素就位于进行起始遍历的位置

算法动画演示

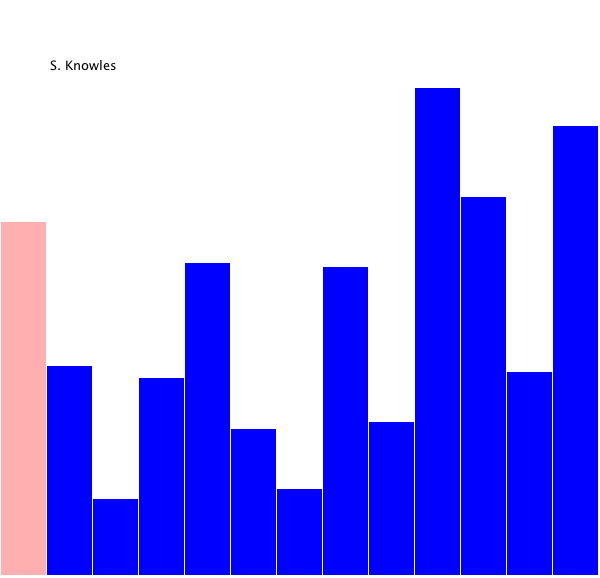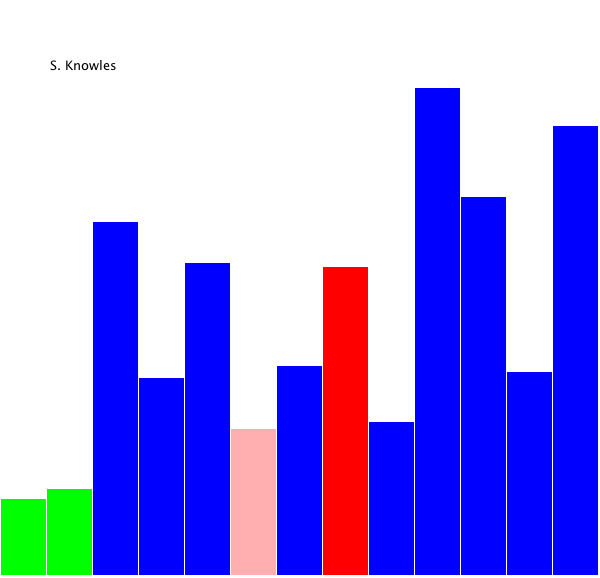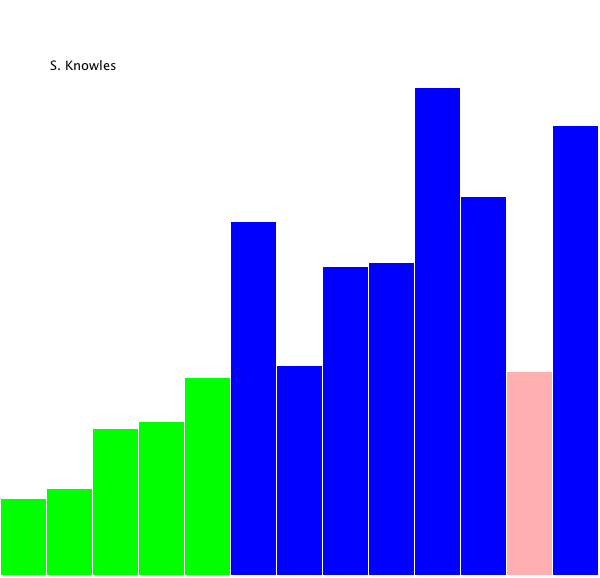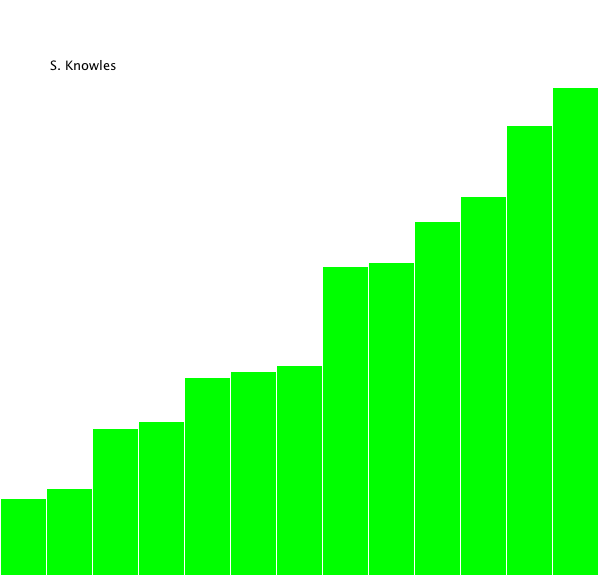
Selection sort

算法实现

SelectionSort.java

import java.util.Random ;
import org.fmz.container.Vector ;
import org.fmz.container.FixedVector ;

public class SelectionSort{

    static void selectionSort(Vector vec){
        int current ; // point to which selection processing(we need process n-1 times)
        int pos ; // in each selection iteation, point to which element we will compare
        int small_pos ; // in each selection iteration, store the smallest element position
        Comparable smallest ; // in each selection iteration, store the smallest element 
        int n = vec.size() ;

        for(current=0; current<n-1; current++){
            small_pos = current ;
            smallest = (Comparable)vec.elementAt(small_pos) ;
            for(pos=current+1; pos<n; pos++){
                if(((Comparable)vec.elementAt(pos)).compareTo(smallest) < 0){
                    small_pos = pos ;
                    smallest = (Comparable)vec.elementAt(pos) ;
                }
            }
            if(small_pos != current)
                swap(vec, current, small_pos) ;
        }    
    }

    static void swap(Vector vec, int first, int last){
        Object temp = vec.elementAt(first) ;
        vec.replace(first, vec.elementAt(last)) ;
        vec.replace(last, temp) ;
    }

    public static void main(String args[]){
        Random rnd = new Random() ;
        FixedVector fvec = new FixedVector() ;
        fvec.append(rnd.nextInt(10)) ;
        fvec.append(rnd.nextInt(10)) ;
        fvec.append(rnd.nextInt(10)) ;
        fvec.append(rnd.nextInt(10)) ;
        fvec.append(rnd.nextInt(10)) ;
        fvec.append(rnd.nextInt(10)) ;
        fvec.append(rnd.nextInt(10)) ;
        fvec.append(rnd.nextInt(10)) ;
        fvec.append(rnd.nextInt(10)) ;
        fvec.append(rnd.nextInt(10)) ;

        selectionSort(fvec) ;
        for(int i=0; i<fvec.size(); i++)
            System.out.print(fvec.elementAt(i) + "\t") ;
    }
}

复杂度分析

The best average worst case for SelectionSort is in O(n^2)

3 插入排序(Insertion Sort)

算法描述

  • 插入排序就像是玩扑克牌一样，我们将新得到的牌与手中的牌(手中的牌已经排好序)对比
  • 找到与得到的牌相比小的牌，即插入这张小牌的后面
  • 后面的牌次序依次后移
  • 经过n-1此之后手中的牌就排好序了

算法动画演示

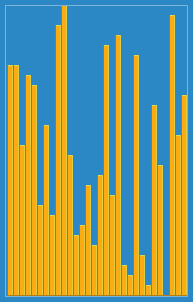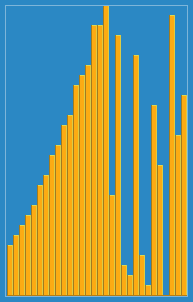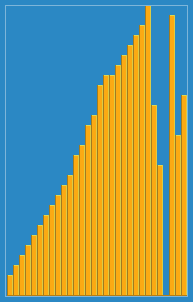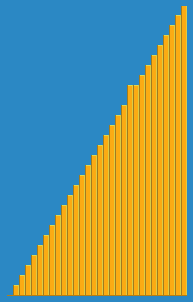
Insertiong Sort

算法实现

InsertionSort.java

import java.util.* ;
import org.fmz.container.Vector ;
import org.fmz.container.FixedVector ;

public class InsertionSort{
    
    static void insertionSort(Vector vec){
        int current ;
        int pos ;
        int n = vec.size() ;
        for(current=1; current<n; current++){
            pos = current ;
            while(pos>0 && ((Comparable)vec.elementAt(current)).compareTo(vec.elementAt(pos-1)) < 0)
                pos -- ;
            if(pos != current){
                vec.insertAt(pos, vec.elementAt(current)) ;
                vec.removeAt(current+1) ;
             }
        }
    }

    public static void insertionSort_v2(int[] array, int lo, int hi){
        int current ;
        int pos ;
        int insert_value ;
        for(current = lo + 1; current < hi; current ++){
            pos = current - 1 ;
            insert_value = array[current] ;
            while(pos >= lo && insert_value < array[pos]){
                array[pos + 1] = array[pos] ;
                pos -- ;
            }
            array[pos + 1]  = insert_value ;
        }
    }

    public static void main(String args[]){
        Random rnd = new Random() ;
        /*
        FixedVector fvec = new FixedVector() ;
        fvec.append(rnd.nextInt(10)) ;
        fvec.append(rnd.nextInt(10)) ;
        fvec.append(rnd.nextInt(10)) ;
        fvec.append(rnd.nextInt(10)) ;
        fvec.append(rnd.nextInt(10)) ;
        fvec.append(rnd.nextInt(10)) ;
        fvec.append(rnd.nextInt(10)) ;
        fvec.append(rnd.nextInt(10)) ;
        fvec.append(rnd.nextInt(10)) ;
        fvec.append(rnd.nextInt(10)) ;
        */
        int[] array = new int[10] ;
        for(int i = 0; i<array.length; i++)
            array[i] = rnd.nextInt(10) ;
        //insertionSort(fvec) ;
        insertionSort_v2(array, 0, array.length) ;
        for(int i : array)
            System.out.print(i + "\t") ;
    }
}

复杂度分析

average case for Insertion Sort in O(n^2)

4 堆排序(Heap Sort)

算法描述

  • 需要构建一个Heap数据结构
  • 将序列添加到MaxHeap中
  • 依次删除MaxHeap的root元素，即为剩余元素中的最大元素

算法动画演示

Max Heap Sort

算法实现

Max Heap Sort

import java.util.Random ;
import org.fmz.container.Vector ;
import org.fmz.container.FixedVector ;
import org.fmz.container.MaxHeap ;

public class HeapSort{

    static void heapSort(Vector vec){
        MaxHeap temp = new MaxHeap(vec.size()) ;
        for(int i=0; i<vec.size(); i++)
            temp.insert((Comparable)vec.elementAt(i)) ;
        for(int i=vec.size()-1; i>=0; i--)
            vec.replace(i, temp.removeMax()) ;
    }
    public static void main(String args[]){
        Random rnd = new Random() ;
        FixedVector fvec = new FixedVector() ;
        fvec.append(rnd.nextInt(10)) ;
        fvec.append(rnd.nextInt(10)) ;
        fvec.append(rnd.nextInt(10)) ;
        fvec.append(rnd.nextInt(10)) ;
        fvec.append(rnd.nextInt(10)) ;
        fvec.append(rnd.nextInt(10)) ;
        fvec.append(rnd.nextInt(10)) ;
        fvec.append(rnd.nextInt(10)) ;
        fvec.append(rnd.nextInt(10)) ;
        fvec.append(rnd.nextInt(10)) ;
        

        heapSort(fvec) ;
        for(int i=0; i<fvec.size(); i++)
            System.out.print(fvec.elementAt(i) + "\t") ;
    }
}

复杂度分析

average case for Heap Sort in O(n*lg(n))

5 归并排序(Merge Sort)

算法描述

  • 归并排序时采用递归的方法进行排序，递归的策略是“分而治之”
  • 直到分解为最小单位为包含一接口一个元素的序列，再进行合并
  • 合并的时候将序列抽离出来为新的序列，同时多加一个哨兵元素，再依次比较两个序列元素的大小，然后替换掉原来的元素进行排序

算法动画演示

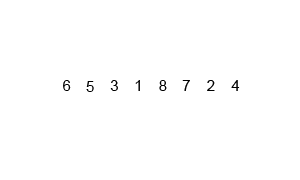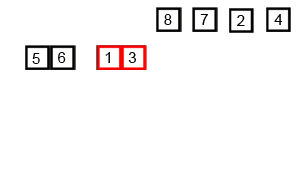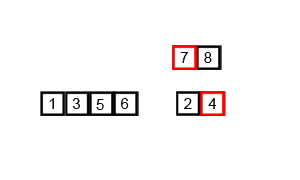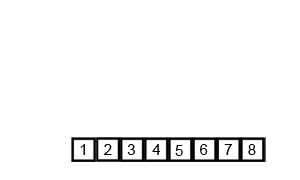
Merge Sort

算法实现

MergeSort.java

import java.util.Random ;

public class MergeSort{

    static void mergeSort(int[] array, int lo, int hi){
        if(lo+1 == hi)
            return ;
        int mid = (lo + hi)/ 2 ;
        mergeSort(array, lo, mid) ;
        mergeSort(array, mid, hi) ;
        merge(array, lo, mid, hi) ;
    }

    static void merge(int[] array, int lo, int mid, int hi){
        int[] array_lt = new int[mid - lo + 1] ;
        int[] array_rt = new int[hi - mid + 1] ;
        for(int i = 0; i < array_lt.length-1; i ++)
            array_lt[i] = array[lo + i] ;
        for(int i = 0; i < array_rt.length-1; i ++)
            array_rt[i] = array[mid + i] ;
        array_lt[array_lt.length-1] = Integer.MAX_VALUE ; // 增加一个哨兵元素
        array_rt[array_rt.length-1] = Integer.MAX_VALUE ; // 增加一个哨兵元素
        int i = 0 ;
        int j = 0 ;
        for(int k = lo; k < hi; k ++){
            if(array_lt[i] < array_rt[j]){
                array[k] = array_lt[i] ;
                i ++ ;
            }else{
                array[k] = array_rt[j] ;
                j ++ ;
            }
        }
    }

    public static void main(String args[]){
        Random rnd = new Random() ;
        int[] array = new int[10] ;
        for(int i = 0; i < array.length; i ++)
            array[i] = rnd.nextInt(10) ;
        mergeSort(array, 0, array.length) ;
        for(int i : array)
            System.out.print(i + "\t") ;
    }
}

复杂度分析

average case for Merge Sort in O(n*lg(n))

6 快速排序(Quick Sort)

算法描述

  • 快速排序和归并和排序相似，是采用分而治之的策略递归进行的
  • 将序列分解成两个相互关联的子序列，在中间找出一个所谓的”pivot”的数
  • 将两个子序列转变成：左边子序列中的每一个元素都小于或者等于”pivot”；右边子序列中的每一个元素都大于或者等于”pivot”。通过方法”medianOf3,partition”完成
  • 递归调用”medianOf3,partition”方法，完成排序

算法动画演示

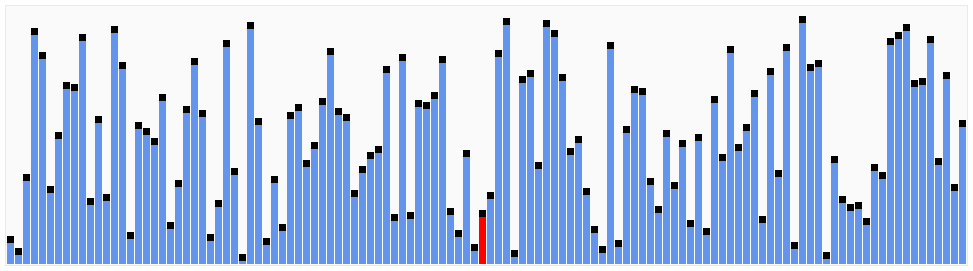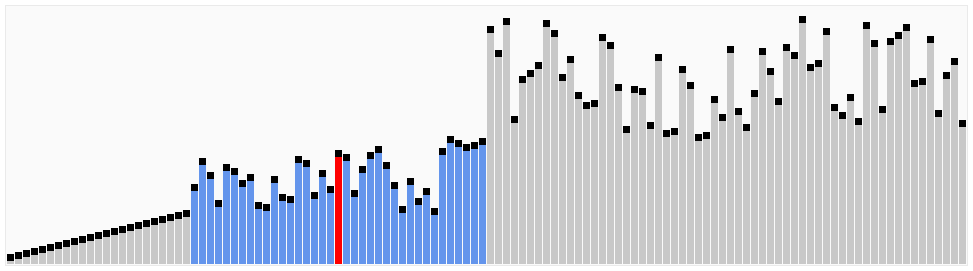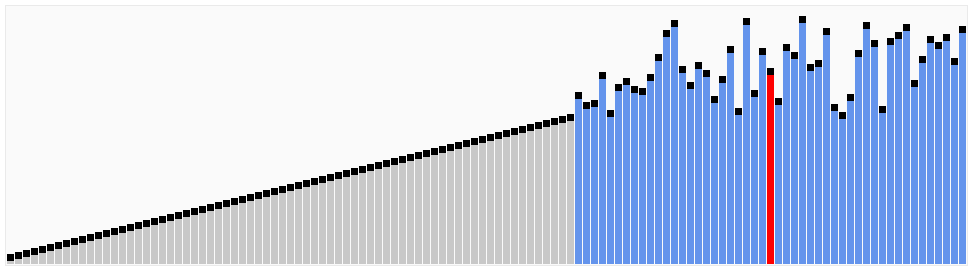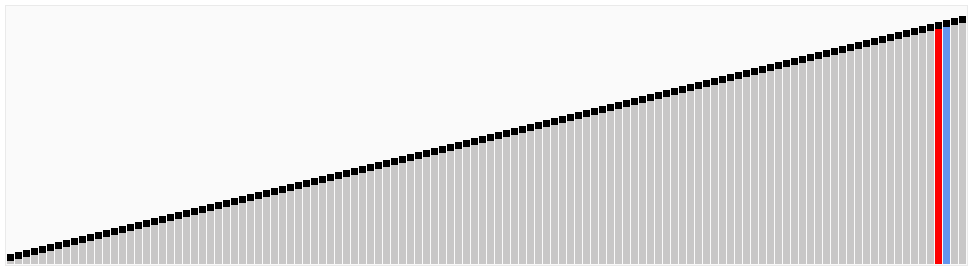
Quick Sort

算法实现

QuickSort.java

import java.util.Random ;

public class QuickSort{

    protected static void swap(int[] array, int first, int last){
        int temp = array[first] ;
        array[first] = array[last] ;
        array[last] = temp ;
    }

    protected static void medianOf3(int[] array, int lo, int hi){
        int mid = (lo + hi) >> 1 ;
        if(array[lo] > array[mid])
            swap(array, lo, mid) ;
        if(array[mid] > array[hi-1])
            swap(array, mid, hi-1) ;
        if(array[lo] > array[mid])
            swap(array, lo, mid) ;
    }

    protected static int partition(int[] array, int lo, int hi){
        int mid = (lo + hi) / 2 ;
        int pivot = array[mid] ;
        while(true){
            while(array[++ lo] < pivot) ;
            while(array[-- hi - 1] > pivot) ;
            if(lo > hi - 1)
                break ;
            else
                swap(array, lo, hi - 1) ;
        }
        return lo ;
    }

    static void quickSort(int[] array, int lo, int hi){
        if(lo - hi <= 10)
            InsertionSort.insertionSort_v2(array, lo, hi) ;
        else{
            medianOf3(array, lo, hi) ;
            int left_prt = partition(array, lo, hi) ;
            quickSort(array, lo, left_prt) ;
            quickSort(array, left_prt + 1, hi - 1) ;
        }
    }

    public static void main(String args[]){
        Random rnd = new Random() ;
        int[] array = new int[50] ;
        for(int i = 0; i < array.length; i ++)
            array[i] = rnd.nextInt(10) ;
        quickSort(array, 0, array.length) ;
        for(int i : array)
            System.out.print(i + ",") ;
    }
}

复杂度分析

average case for Quick Sort is in O(n*lg(n))

7 Shell排序(Shell Sort)

算法描述

  • Shell排序算法是以它的发明者D.L.Shell命名的
  • Shell算法是Insertion Sort算法的推广
  • 算法的关键是使用了”h-increment”，也就是相当于在间隔h的元素上进行Insertion Sort
  • h的值不断变小，最后变成了1，也就是完全意义上的Insertion Sort

算法动画演示

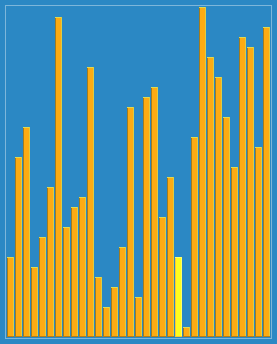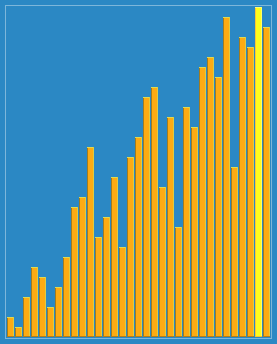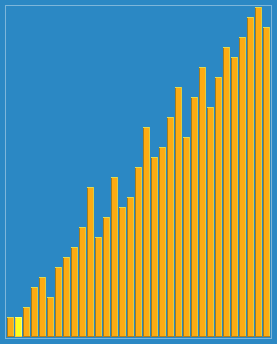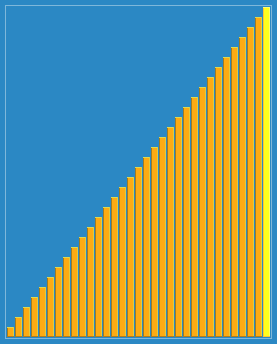
Shell Sort

算法实现

ShellSort.java

import java.util.Random ;

public class ShellSort{

    static void shellSort(int[] array, int lo, int hi){
        int current ;
        int pos ;
        int insert_value ;
        int h = 1 ;
        while(h < hi)
            h = h * 3 + 1 ;

        while(h > 0){
            for(current = h; current < hi && current >= lo; current ++){
                insert_value = array[current] ;
                pos = current ;
                while(pos > h - 1 && insert_value < array[pos - h]){
                    array[pos] = array[pos - h] ;
                    pos -= h ;
                }
                array[pos] = insert_value ;
            }
            h = (h - 1) / 3 ;
        }
    }

    public static void main(String args[]){
        Random rnd = new Random() ;
        int[] array = new int[20] ;
        for(int i = 0; i < array.length; i ++)
            array[i] = rnd.nextInt(10) ;
        shellSort(array, 0, array.length) ;
        for(int i : array)
            System.out.print(i + ",") ;
    }

}

复杂度分析

利用sequence[1, 2, 8, 2^(k-1),.]，the Shell Sort is in O(n^1.5)

End
← 上一页 下一页 →