整数、浮点数及字符在计算机中的数据表示教程

目录

• 1 数字系统
  • 1.1 十进制
  • 1.2 二进制
  • 1.3 十六机制
  • 1.4 不同进制间的转化
• 2 计算机存储和数据表示
• 3 整数表示
  • 3.1 n-bit无符号整数
  • 3.2 n-bit无符号整数
  • 3.3 用Sign-Magnitude的方式表示n个字节的有符号整数
  • 3.4 用1’s-complement的方式表示n个字节的有符号整数
  • 3.5 用2’s-complement的方式表示n个字节的有符号整数
  • 3.6 计算机使用2’s-complement的方式来表示有符号的整数
  • 3.7 2’s-complement数值表示范围
  • 3.8 Big Endia Vs. Little Endian
• 4 浮点数表示
  • 4.1 IEEE-754 32-bit单精度浮点数
  • 4.2 IEEE-754 64-bit双精度浮点数
  • 4.3 Special Vlaue
• 5 字符集&字符编码
  • 5.1 字符集VS字符编码
  • 5.2 7-bit ASCII Code(aka US-ASCII, ISO/IEC 646, ITU-T T.50)
  • 5.3 8-bit Latin-1(aka ISO/IEC 8859-1)
  • 5.4 US-ASCII(ASCII Extensions)的其他8-bit扩展
  • 5.5 Unicode(aka ISO/IEC 10646 Universal Character Set)
  • 5.6 UTF-8(Unicode Transformation Format - 8-bit)
  • 5.7 多字节型字符表示的文档文件
  • 5.8 完档文件的格式

1 数字系统

也许是因为人类有10个手指和两个大拇指，所以我们用常用十进制和十二进制。计算机为了方便设计，只认识0和1，也就是使用二进制。在计算机科学中，为了表示的方便，我们也经常使用十六机制(hexadecimal)或者八进制(octal)用来表示二进制的数字。

1.1 十进制

我们使用10个符号来表示十进制：

0 1 2 3 4 5 6 7 8 9

它们使用位置记号，不同的位置有不同的量级：

1234 = 1*10^3 + 2*10^2 + 3*10^1 + 4*10^0

为了避免混淆，在必要的时候我们将十进制的数据前边加一个前缀D

1.2 二进制

我们使用2个符号来表示十进制：

0 1

它们使用位置记号，不同的位置有不同的量级：

1234 = 1*2^3 + 2*2^2 + 3*2^1 + 4*2^0

我们使用前缀B来避免混淆。在一些编程语言中我们也使用前缀0b，例如：0b10010011；或者使用前缀b，例如：b'10010011'

1.3 十六进制

我们使用16个符号来表示十进制：

0 1 2 3 4 5 6 7 8 9 A B C D E F

它们使用位置记号，不同的位置有不同的量级：

1234 = 1*16^3 + 2*16^2 + 3*16^1 + 4*16^0

我们使用前缀H来避免混淆。在一些编程语言中我们也使用前缀0x，例如：0x10010011；或者使用前缀x，例如：x'10010011'

1.4 不同进制之间的转化

二级制转换为十六机制

• 从右到左将4-bit划分为一组
• 左边最后不够4-bit用0补充
• 将每4-bit转化为一个十六进制的数字

1001001010B = 0010 0100 1010B = 24AH

将十进制(base 10)转化为其他进制(base r)

将261D转化为十六进制：

• 261/16 => 除数=16，余数=5
• 16/16 => 除数=1，余数=0
• 1/16 => 除数=0，余数=1；当除数是0的时候算法终止

因此，261D=105H

将1023(base 4)转化为base 3：

• 1023(base 4)/3 => 除数=25D，余数=0
• 25/3 => 除数=8D，余数=1
• 8/3 => 除数=2D，余数=2
• 2/3 = 除数=0D，余数=2；当除数是0的时候算法终止

因此，1023(base 4)=2210(base 3)

浮点数转化为其他制

1. 把整数部分和小数部分分开
2. 对于整数部分，除以目标基数，逆向取得所得的余数
3. 对于小数部分，不断用基数乘以小数部分，正向取得所得到的整数部分

将18.6875转化为二级制

• 整数部分18

  • 18/2 => 除数=9，余数=0
  • 9/2 => 除数=4, 余数=1
  • 4/2 => 除数=2，余数=0
  • 2/2 => 除数=1，余数=0
  • 1/2 => 除数=0，余数=1，terminate
  • 因此，18D=10010B

• 小数部分0.6875

  • 0.6875 * 2 = 1.375， 整数部分是1
  • 0.375 * 2 = 0.75， 整数部分是0
  • 0.75 * 2 = 1.5， 整数部分是1
  • 0.5 * 2 = 1.0， 整数部分是1
  • 因此，0.6875D=0.1011B

因此，18.6875D = 10010.10011B

十六进制也可以同样进行转化

2 计算机存储和数据表示

计算机使用固定数量的bit来表示数据，这个数据可以是数字、字符或者其他。一个n-bit大小的储存可以代表2^n个不同的条目。

就整数来说，可以用16-bit、32-bit或者64-bit来表示。程序员负责来选择到底使用哪一种bit长度，不同的bit长度会限制整数的表示范围。整数可以用不同的表达范式(representation shceme)来表示，例如无符号(Unsigned)和有符号(Signed)。

计算机储存的只是二进制的数据，至于数据怎么被读取，完全决定于你。例如，8-bit二进制数据0100 0001B可以被解释成无符号的数字65，也可以被解释成ASCII编码的'A'。

罗塞塔石碑和埃及象形文字的解读

公元前4000年开始，古埃及人就开始使用象形文字。不幸的是，公元500年之后就没有人能够理解这种文字了，这种情况一致持续到1799拿破仑的远征部队占领埃及时在尼罗河三角洲的罗塞塔小镇上意外挖到了一块黑色的大石头。

罗塞塔石碑上刻的是公元前196年国王托米勒五世颁布的诏令，共有三种语言刻在石碑上。从上到下依次是：古埃及象形语、古埃及草书(平民使用的文字)和古希腊语言。它们都表示同样诏书的意思，而人们能看懂古希腊语言，这就成为了人们解密古埃及象形语的关键一把钥匙。

悲伤的故事告诉我们：除非你知道编码范式，否则你无法解码数据。

罗塞塔石碑

古埃及象形文字

3 整数表示

在计算机当中整数的表示和浮点数的表示是完全不同的

整数通常使用8-bit、16-bit、32-bit、64-bit来表示，表示的范式有两种：

• 无符号整数(UNSIGNED INTEGER)：可以用来表示0和正数
• 有符号整数(SIGNED INTEGER)：可以用来表示负数、0和正数，有三种不同的表示方法:
  • Sign-magnitude representation
  • 1’s complement representation
  • 2’s complement representation

3.1 n-bit无符号整数

n-bit无符号整数表示方法可以用来表示2^n个数值，从0到2^n-1，最大值是2^n-1，最小值是0

3.2 有符号整数

有符号整数可以用来表示负数、0和正数，有三种不同的表示方法：

1. Sign-Magnitude representation
2. 1’s complement representation
3. 2’s complement representation

当我们用字节(实际上是多个bit)表示一个整数的时候，我们把第一个bit称为：msb(most-significant-bit)，我们把最后一个bit称为：lsb(least-significant-bit)

在所有表示整数的不同范式中，msb是符号字节(sign bit)。如果符号字节是0，表示正整数；如果符号是1，表示负整数。

3.3 用Sign-Magnitude的方式表示n个字节的有符号整数

• 符号字节为0表示为正整数，符号字节为1表示为父整数
• 除了第一个符号字节(msb)的其他n-1个字节代表数值真实的量

例如：

• 0 100 0001B(8-bit) 表示 +65D，其中0代表的是+的意思，后边的字节表示数值的量

• 1 000 0001B(8-bit) 表示 -1D，其中1代表的是-的意思，后边的字节表示数值的量

• 0 000 0000B(8-bit) 表示 +0D，…

• 1 000 0000B(8-bit) 表示 -0D，…

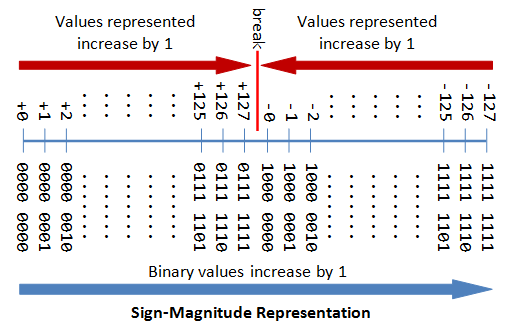
Sign-magnitude数值表示的缺点：

1. 有两中表示都是表示的0，造成低效和混淆
2. 正数和负数需要分开来处理

3.4 用1's-complement的方式表示n个字节的有符号整数

• 同样，符号bit为0表示为正整数，符号bit为1表示为负整数
• 除了第一个符号字节(msb)的其他n-1个字节代表数值真实的量
  • 对于正整数，其量就等于剩余的字节的量
  • 对于负整数，其量等于剩余的n个字节翻转后(0变为1,1变为0)后的量

例如：

• 0 100 0001B(8-bit) 表示 +65D，其中0代表的是+的意思，后边的字节表示数值的量

• 1 000 0001B(8-bit) 表示 -126D，其中1代表的是-的意思，后边的字节翻转后为111 1110的量

• 0 000 0000B(8-bit) 表示 +0D，…

• 1 000 0000B(8-bit) 表示 -0D，…

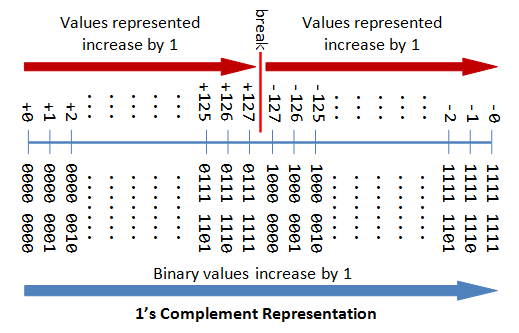
Sing-magnitude数值表示的缺点：

1. 有两中表示都是表示的0，造成低效和混淆
2. 正数和负数需要分开来处理

3.5 用2's-complement的方式表示n个字节的有符号整数

• 同样，符号字节为0表示为正整数，符号字节为1表示为负整数
• 除了第一个符号字节(msb)的其他n-1个字节代表数值真实的量
  • 对于正整数，其量就等于剩余的字节的量
  • 对于负整数，其量等于剩余的n个字节翻转后(0变为1,1变为0)后的量再加上1

例如：

• 0 100 0001B(8-bit) 表示 +65D，其中0代表的是+的意思，后边的字节表示数值的量

• 1 000 0001B(8-bit) 表示 -127D，其中1代表的是-的意思，后边的字节翻转后为111 1110的量加1

• 0 000 0000B(8-bit) 表示 +0D，…

• 1 000 0000B(8-bit) 表示 -128D，其中1代表的是-的意思，后边的字节翻转后为111 1111的量加1

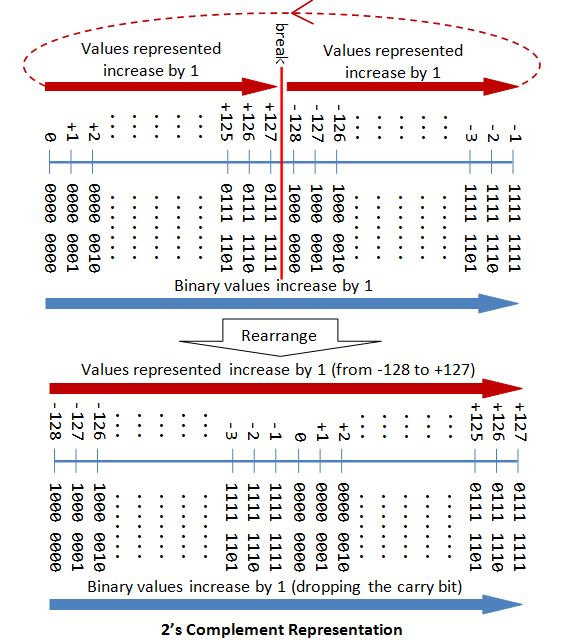
3.6 计算机使用2's-complement的方式来表示有符号的整数

在计算机科学当中，我们使用2’s-complement的方式来表示有符号的整数，那么因为：

1. 在2’s-complement的表示方式中，我们只有一个0
2. 在加法和减法的运算当中，整数和负数可以被同样的对待，也就是说我们可以用将之应用到”加法逻辑”当中

例如：

65D ->      0100 0001B
5D  ->      0000 0101B(+
=           0100 0111B

65D ->      0100 0001B
-5D ->      1111 1011B(+
=           0011 1100B

固定bit的整数都有自己的范围，当我们在进行运算的时候，要记得查询计算的数值是否越界

下图表示三种有符号整数表示范式的变迁：

3.7 2's-complement数值表示范围

用2’s-complement方法来表示一个有符号整数的表示范围是-2^(n-1) ~ +(2^(n-1)-1)，最大值2^(n-1)-1 + 1等于最小值-2^(n-1)

3.8 Big Endia Vs. Little Endian

现代的计算机在一个内存地址(memory address)中储存一个字节(8bit)，因此一个32-bit的整数需要4个内存地址。那么这些字节是以什么样的顺序储存的呢？

Big Endia是指msb储存在最低位的地址当中(big in first)；Small Endian是指lsb储存在最低位的地址当中(small in first)

例如，一个32-bit的整数12345678H在计算机内存内存当中的储存是：12H 34H 56H 78H(Big Endian)；78H 56H 34H 12H(Small Endian)

4 浮点数表示

浮点数使用科学计数的方法进行表示，包含小数部分(F)，基数(radix)部分(r)和基数的指数部分(E)，表示的方式是F * r^E。对于十进制数据就是：F * 10^E；对于二进制数据就是：F * 2^E

浮点数的表示并不唯一，比如55.66可以表示成：5.566 * 10^1 、0.5566 * 10^2、0.05566 * 10^3…。小数的部分可以被归一化，例如123.4567可以归一化为1.234567 * 10^2；1010.1011B可以归一化为1.0101011 * 2^3

值得注意的是：当我们用固定的bit来表示一个浮点数的时候，我们往往会丢失精度。真实世界的数据有无穷多个，而n-bit只能表示2^n个数值。浮点数的表示只能尽可能的近似，而不能表达全部。

4.1 IEEE-754 32-bit单精度浮点数

• msb是符号位，0表示整数，1表示负数(第1位)
• 接下来的8-bit表示指数exponet(E)(中间8位)
• 剩下的23-bit表示小数fraction(F)(最后23位)

例如：计算32-bit1 1000 0001 011 0000 0000 0000 0000 0000

• 1 -> 表示负数

011 0000 0000 0000 0000 00000 -> 表示小数部分，默认的小数部分的整数是1。也就表示1.011 0000 0000 0000 0000 0000 = 1 + 1 * 2^-2 + 1 * 2^-3 = 1.375D

• 1000 0001 -> 表示指数部分，在归一化的形式中，真正的指数是E-127，这是因为用8-bit我们需要表达正的指数也需要表达负的指数。1000 0001 = 129D，此处：E=129D-127D=2D

• 因此表达的浮点数是：-1.375 * 2^2 = -5.5D

总结：

• 当1<=E<=254时候，N=(-1)^s * 1.F * 2^(E-127)
• 当E=0时候，N=(-1)^s * 0.F * 2^(-126)，这些数用来表示非常接近0的数
• 当E=255时候，代表特定的数，例如+(-)INF和NAN(not a number)

4.2 IEEE-754 64-bit双精度浮点数

• msb是符号位，0表示整数，1表示负数(第1位)
• 接下来的11-bit表示指数exponet(E)(中间11位)
• 剩下的52-bit表示小数fraction(F)(最后52位)

总结：

• 当1<=E<=2046时候，N=(-1)^s * 1.F * 2^(E-1023)
• 当E=0时候，N=(-1)^s * 0.F * 2^(-1022)，这些数用来表示非常接近0的数
• 当E=2047时候，代表特定的数，例如+(-)INF和NAN(not a number)

4.3 Special Value

Zero

zero不能用归一化的形式来表示，必须用非归一化的形式E=0，F=0，有两种0，+0和-0

Infinity

正infinity(e.g.,1/0)表示为E=255(32-bit)或者E=2047(64-bit)，F=0，S=0

负infinity(e.g.,1/0)表示为E=255(32-bit)或者E=2047(64-bit)，F=0，S=1

Not a Number

不能表示为一个确切的数(e.g.,0/0)，E=255(32-bit)或者E=2047(64-bit)，F是任何的non-zero小数

5 字符集&字符编码

最常用的字符编码方式是：7-bit ASCII(ISO/IEC 646)和8-bit Latin-x(ISO/IEC 8895-x)，这些编码主要用来表示西欧的字符；Unicode(ISO/IEC 10646)是为了表示国际化字符。

5.1 字符集VS字符编码

所谓的字符集可以理解为一种规范，它定义了一个字符和对应表示这个字符的数值(Code Point)。而字符编码是描述怎么将字符集的Code Point用在计算机中存储起来。

字符集可以看做一个字典，根据一个字符可以查找到对应的数值，怎么把数值存储在计算机中呢？需要用一定的编码格式，为什么呢？因为，有的值(Code Point)用一个字节(byte)可以表示，有的值至少用两个字节(byte)，要定义好编码规则，才能有效读取存储的数据。

ASCII和ISO-8859-X似乎字符集和字符编码时一回事啊？是的，因为这两个字符集的最大长度是一个字节，那么我们可以直接用字符集的Code Point的数值表示在计算机中存储起来，所以没有编码一说；而对于Unicode字符集来说，字符集对应的Code Point最大值要大于两个字符，这时候就需要定义编码格式，才能有效的编码和解码数据。于是就有了不同的实现：UTF-8(可变字符，1-3 byte)，UTF-16(可变字符，2 bytes OR 4 bytes)和UTF-32(4 bytes)。

5.2 7-bit ASCII Code(aka US-ASCII, ISO/IEC 646, ITU-T T.50)

ASCII(American Standard Code for Information Interchange)是比较早的一种字符表示方式。现在的ASCII已经扩展到了8-bit，这样能够更好的利用计算机8-bit作为一个memory address的特点

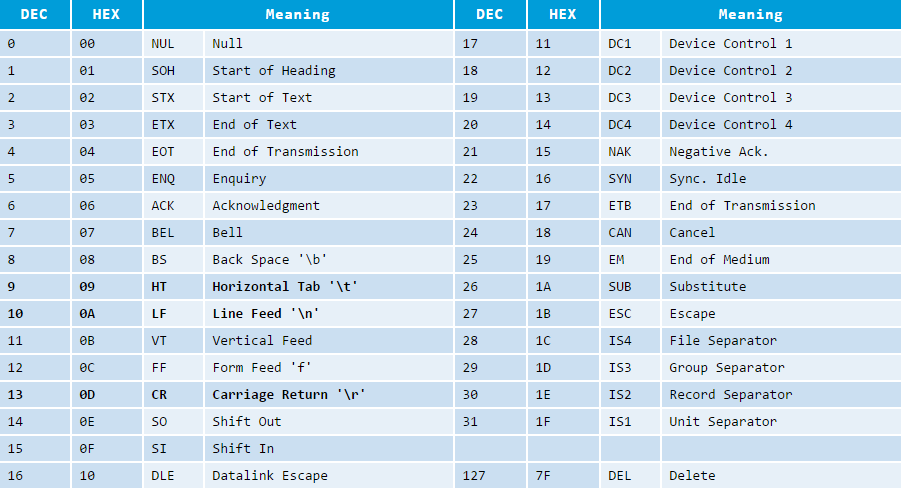
ASCII的可打印字符表：

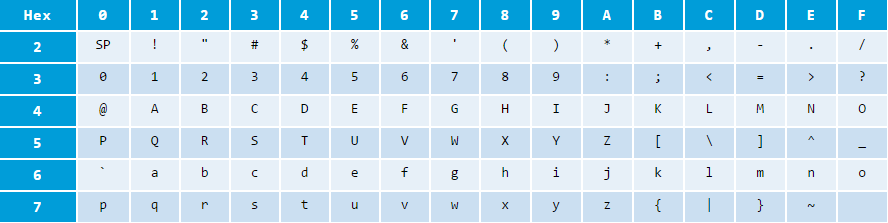
• ‘0’ to ‘9’: 30H-39H(48D-57D)，中间没用gap
• ‘A’ to ‘Z’: 41H-5AH(65D-90D)，中间没有gap
• ‘a’ to ‘z’: 61H-7AH(97D-122D)，中间没有gap

ASCII共95个可打印字符

ASCII不可打印字符表：

5.3 8-bit Latin-1(aka ISO/IEC 8859-1)

ISO/IEC-8859是西方语言的标准。ISO/IEC 8859-1又称为Latin alphabet No.1或者是Latin-1，Latin-1共有191个可打印字符，向后兼容ASCII编码。主要覆盖的语言有：英语、德语、意大利语、葡萄牙语和西班牙语

Latin-1可打印字符表(省略ASCII可打印字符)：

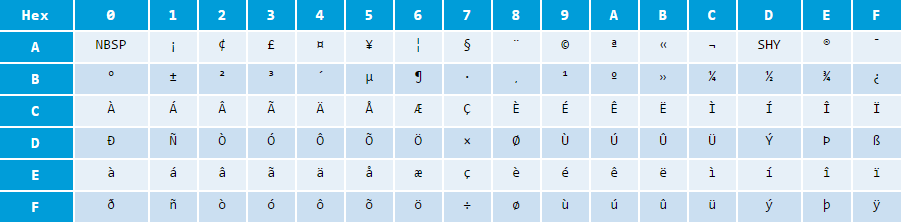
ISO/IEC=8895共分为16个部分，最常用的是Part 1，Part 2主要覆盖中欧(波兰、捷克、匈牙利等)，Part 3主要覆盖南欧(土耳其等)，Part 4主要覆盖北欧(爱沙尼亚、拉脱维亚等)，Part 5主要是为西里尔字母，Part 7主要是为希腊，Part8主要是为希伯来人(以色列)，Part 9主要是为土耳其，Part 10主要是为北欧人，Part 11主要是为泰国，Part 12已经被抛弃，Part 13主要是为波罗的海沿岸，Part 14主要是为赛尔特语，Part 15主要是为法国、芬兰等，Part 16主要是为欧洲东南部。

5.4 US-ASCII(ASCII Extensions)的其他8-bit扩展

ANSI(American National Standard Institude)(aka Windowns-1252)是8-bit的字符集，也是Latin-1的一个超集，它定义了128D(80H)到159D(9FH)之间的字符为”Displayable Character”，例如：”smart” 单引号等

常常出现的问题是：在web浏览器中，我们使用的微软的一些产品所有的引号和单引号都被制作成”smart”，但是文档的字符集是Latin-1，所以会出现一部分乱码的现象。

Windowns-1252部分字符表：

5.5 Unicode(aka ISO/IEC 10646 Universal Character Set)

Unicode试图提供一个标准的字符集，这个字符集同样是国际化的、有效的、统一的和不易混淆的。

Unicode向后兼容7-bit ASCII 和8-bit Latin-1。也就是说开始的126个字符和US-ASIII是一样的，开始的256个字符和Latin-1是一样的

Unicode最初使用16 bits(称之为UCS-2或者Unicode Character Set-2)，能够表示65,536个字符。后来Unicode扩展到目前的21 bits(能够表达两百多万个字符)。65536个字符我们称之为Basic Multilingual Plane(BMP)，这6万多个字符之外的字符称之为Supplementary Characters，这些字符并不常用。

Unicode有两种编码的方式：

• UCS-2(Universal Character set - 2 Byte): 用16 bits来包含BMP(65536个字符)，UCS-2已经过时了。
• UCS-4(Universal Character set - 4 Byte): 包含了BMP和Supplementary Characters。

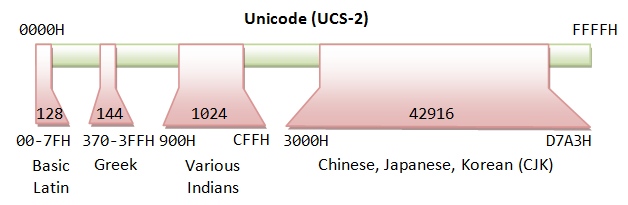
Unicode BMP(基本面)

Unicode将所有的字符定义为17个平面(code area)，其中第一个也是最重要的一个面叫做基本面(BMP, Basic Multilingual Plane)，定义了从U+0000 ~ U+FFFF的数值。各个国家常用的字符都包含在BMP之内。

5.6 UTF-8(Unicode Transformation Format - 8-bit)

Unicode效率非常低，因为如果一个文档大部分包含ASCII字符，每一个字符需要用2个或者4个字节来表示，就造成了大量的空间浪费。因此UTF-8使用可变字节表示的编码方式，用1-4个字节来表示一个字符。

Unicode和UTF-8之间的转化：

UTF-8是用1-3个字节来表示BMP(16-bit)，并且用4-bit来表示Supplementary Characters(21-bit)

128 ACSII字符(拉丁字符、数字和标点)使用1个Byte；扩展的拉丁字符、希腊字符、亚美尼亚语、希伯来语、阿拉伯语使用2个字节；中文、日本语和韩语(CJK)用3个字节。

5.7 多字节型字符表示的文档文件

BOM(Byte Order Mark)

BOM用来标记big-endian储存和small-endian储存。当BOM是FE FFH时候，表明文档是Big-Endian储存的；当BOM是FF FEH时候，表明文档是Small-Endian储存的

UTF-8的文档默认是Big-Endian储存的。然而在Windows系统中，BOM作为最开始的字节加入文件，在UTF-8的文档中加入BOM是不推荐的，这样容易在其他的操作系统中产生混乱，Windows将FE FFH编码为EF BB BF插入文件的头(.txt文件的UTF-8格式默认含有BOM)，在Windows下最好选择没有BOM的UTF-8文件(可以采用其他字符编辑器Notepad)

5.8 文档文件的格式

• Windowns/DOS 使用0D0AH(CR+LF or \r\n)作为EOL(End Of Line)
• Unix和Mac使用0AH(LF or \n)作为EOL

Referece:

• http://www.ntu.edu.sg/home/ehchua/programming/java/datarepresentation.html

疑问？勘误？

• 文章底部评论区欢迎留言
• 微信搜索公众号“冯兄画戟”并留言。
• 邮箱私信：fengmengzhao@gmail.com