机器学习(北京培训)

目录

• 0 前言
• 1 机器学习的基础原理
  • 1.1 基本概念
  • 1.2 典型应用
  • 1.3 预备知识
    • 1.3.1 向量空间模型
    • 1.3.2 信息论
• 2 机器学习常用技术之分类
  • 2.1 文本分类
  • 2.2 朴素贝叶斯(Naive Bayes)分类器
  • 2.3 中心向量分类器
  • 2.4 KNN分类器
  • 2.5 线性分类器
  • 2.6 感知机
  • 2.7 支持向量机
    • 2.7.1 线性可分支持向量机
    • 2.7.2 线性支持向量机
    • 2.7.3 非线性支持向量机
  • 2.8 其他分类方法
    • 2.8.1 决策树方法
    • 2.8.2 回归方法
    • 2.8.3 基于投票的方法(集成方法)
    • 2.3.4 多类下的单标签和多标签问题
• 3 聚类问题
  • 3.1 聚类的评价
  • 3.2 K-Means聚类方法
  • 3.3 层次聚类
  • 3.4 其他聚类方法
• 4 回归
• 5 推荐

---

---

0 前言

机器学习的书籍推荐：

• 李航著，《统计学习方法》，清华大学出版社，2012年3月
• 周志华著，《机器学习》，清华大学出版社，2016年1月

机器学习推荐工具：

• Python scikit-learn
• Weka(Java)
• Mahot(Java)
• 开源项目和工具

数据工程师的基本能力：

• 数据操作能力
  • 数据类型
    • SQL
    • NoSQL
    • Raw files
  • ETL
    • 可能占据80%的时间
    • 需要掌握一种通用语言
• 基本的编程能力
  • C++ Python Java
• 统计学习知识
  • 基本概念
  • 常用手段
• 机器学习的基本算法
  • 原理
  • 应用

大数据工程师的基本能力：

• 分布式计算能力
  • 工程能力
    • 分布式数据操控能力
    • Hadoop/Storm/Spark环境下的应用开发
  • 机器学习的算法能力
    • 常用算法的并行化原理
    • 常见分布式计算软件包应用能力

1 机器学习的基础原理

1.1 基本概念

什么是机器学习？

机器学习是研究如何”利用从数据中得来的经验来改善计算机系统自身的性能”

• Learning : improving some performance measure with experience accumulated/computed from observation
• Machine Learning: improving some performance measure with experience computed from data

什么是数据挖掘？

数据挖掘是：识别出巨量知识中有效的、新颖的、潜在有用的、最终可以理解的模式的平凡过程。

数据挖掘也常常被称之为知识发现(Knowledge Discovery)

机器学习和数据挖掘的关系：

数据挖掘技术包括：数据分析技术 + 数据管理技术。机器学习提供的是数据分析技术，所以，机器学习是数据挖掘的一部分。

机器学习和其他学科的关系：

模式识别=机器学习。两者的主要区别在于前者是从工业界发展起来的概念，后者则主要源自计算机学科。在著名的 《Pattern Recognition And Machine Learning》这本书中，Christopher M. Bishop在开头是这样说的“模式识别源自工业界，而机器学习来自于计算机学科。不过，它们中的活动可以被视为同一个领域的两个方面，同时在过去的10 年间，它们都有了长足的发展”。

数据挖掘=机器学习+数据库。这几年数据挖掘的概念实在是太耳熟能详。几乎等同于炒作。但凡说数据挖掘都会吹嘘 数据挖掘如何如何，例如从数据中挖出金子，以及将废弃的数据转化为价值等等。但是，我尽管可能会挖出金子，但我也可能挖的是“石头”啊。这个说法的意思 是，数据挖掘仅仅是一种思考方式，告诉我们应该尝试从数据中挖掘出知识，但不是每个数据都能挖掘出金子的，所以不要神话它。一个系统绝对不会因为上了一个 数据挖掘模块就变得无所不能(这是IBM最喜欢吹嘘的)，恰恰相反，一个拥有数据挖掘思维的人员才是关键，而且他还必须对数据有深刻的认识，这样才可能从 数据中导出模式指引业务的改善。大部分数据挖掘中的算法是机器学习的算法在数据库中的优化。

统计学习近似等于机器学习。统计学习是个与机器学习高度重叠的学科。因为机器学习中的大多数方法来自统计学，甚 至可以认为，统计学的发展促进机器学习的繁荣昌盛。例如著名的支持向量机算法，就是源自统计学科。但是在某种程度上两者是有分别的，这个分别在于：统计学 习者重点关注的是统计模型的发展与优化，偏数学，而机器学习者更关注的是能够解决问题，偏实践，因此机器学习研究者会重点研究学习算法在计算机上执行的效 率与准确性的提升。

计算机视觉=图像处理+机器学习。图像处理技术用于将图像处理为适合进入机器学习模型中的输入，机器学习则负责 从图像中识别出相关的模式。计算机视觉相关的应用非常的多，例如百度识图、手写字符识别、车牌识别等等应用。这个领域是应用前景非常火热的，同时也是研究 的热门方向。随着机器学习的新领域深度学习的发展，大大促进了计算机图像识别的效果，因此未来计算机视觉界的发展前景不可估量。

语音识别=语音处理+机器学习。语音识别就是音频处理技术与机器学习的结合。语音识别技术一般不会单独使用，一般会结合自然语言处理的相关技术。目前的相关应用有苹果的语音助手siri等。

自然语言处理=文本处理+机器学习。自然语言处理技术主要是让机器理解人类的语言的一门领域。在自然语言处理技 术中，大量使用了编译原理相关的技术，例如词法分析，语法分析等等，除此之外，在理解这个层面，则使用了语义理解，机器学习等技术。作为唯一由人类自身创 造的符号，自然语言处理一直是机器学习界不断研究的方向。按照百度机器学习专家余凯的说法“听与看，说白了就是阿猫和阿狗都会的，而只有语言才是人类独有 的”。如何利用机器学习技术进行自然语言的的深度理解，一直是工业和学术界关注的焦点。

什么是大数据？

• 4V 理论
  • 海量的数据规模(volume)
  • 快速的数据流转和动态的数据体系（velocity）
  • 多样的数据类型（variety）
  • 巨大的数据价值（value）

大数据和机器学习的关系？

大数据相关的技术包括很多方面：数据的获取、数据的存储和数据的分析。在数据的分析这块中，主要包括高性能计算和机器学习两个方面。

总之，大数据不仅仅是机器学习，还包括编程语言、软件开发、概率统计、分布式计算、云计算、可视化…

什么是深度学习？

深度学习时机器学习的一个分支，可以理解为特征学习(feature learning)或者说是表示学习(representation learning)的一种学习方法。

深度学习近年来在图像、语音等领域获得应用，效果显著提升

机器学习的分类方法：

• 机械学习（Rote learning）：学习者无需任何推理或其它的知识转换，直接吸取环境所提供的信息。如塞缪尔的跳棋程序。
• 示教学习（Learning from instruction）：学生从环境（教师或其它信息源如教科书等）获取信息，把知识转换成内部可使用的表示形式，并将新的知识和原有知识有机地结合为一体。
• 类比学习（Learning by analogy）：利用二个不同领域（源域、目标域）中的知识相似性，可以通过类比，从源域的知识（包括相似的特征和其它性质）推导出目标域的相应知识，从而实现学习。例如，一个从未开过货车的司机，只要他有开小车的知识就可完成开货车的任务。
• 归纳学习（Learning from induction）：教师或环境提供某概念的一些实例或反例，让学生通过归纳推理得出该概念的一般描述。

归纳学习方法的分类：

• 监督学习(Supervised Learning)：也称为有监督学习，是从标记(label)或者说标注的训练数据(或者说样本)中来进行推断的机器学习任务。如分类、回归。
• 非监督学习(Unsupervised Learning)：也称无监督学习，它的问题是，在未标记的数据中，试图找到隐藏的结构。如聚类、密度估计。
• 强化学习(Reinforcement Learning)：强化学习是机器学习中的一个领域，强调如何基于环境而行动，以取得最大化的预期利益。

半监督学习的特点：

• 监督学习需要标记大量的样本，而非监督学习准确性有待提高。
• 随着信息技术的发展，收集大量未标记样本已相当容易，而获取大量有标记的样本则相对较为困难，因为获得这些标记可能需要耗费大量的人力物力。
• 如何利用大量的未标记样本来改善学习性能成为当前机器学习研究中备受关注的问题。
• 半监督学习：学习器通过对有少量带标记的样本和大量未标记的样本的学习，建立模型用于预测未见样本的标记。

机器学习的基本过程：

表示- –> *训练- –> *测试

• 表示：将数据对象进行特征化处理
• 训练：给定一个数据样本集，从中学习出规律（模型
  • 目标：该规律不仅适用于训练数据，也适用于未知数据(称为泛化能力)
• 对于一个新的数据样本，利用学到的模型进行预测

表示的过程是和行业相关的重要的过程，一般需要行业专家级从业人员从中给出建议。

训练的过程是如何找出规律的过程，包括三个部分：模型、策略和算法。

• 模型：确定要找的是哪类规律（函数形式）或者说假设空间，比如线性函数
• 策略：从众多可能的规律中选出最好的选择标准，比如某个损失函数最小
• 算法：如何快速寻找到最好结果，比如梯度法、牛顿法

测试的过程是根据找到规律进行预测，预测的好与坏需要一个标准，一般采用打分的方法来进行测试的评价。

1.2 典型应用

列举一些机器学习的典型应用：

• 网页分类
• 人脸识别
• 搜索引擎排序结果
• 垃圾邮件过滤
• 机器翻译
• 文档自动摘要
• 手写识别
• 图像去噪
• 视频跟踪和智能事件分析
• 推荐系统
• 计算广告

1.3 预备知识

1.3.1 向量空间模型

向量空间模型(Vector Space Model，VSM)由康奈尔大学 Salton等人上世纪70年代提出并倡导。

每篇文档(或者每个查询)都可以转化为一个向量，于是文档之间或文档和查询之间的相似度可以通过向量之间的距离来计算。

用于文本分析时，向量中的每一维对应一个词项(term)或者说文本特征。

n篇文档，m个词项构成的矩阵Am*n，每列可以看成每篇文档的向量表示，同时，每行也可以可以看成词项的向量表示：

\[A_{m*n} = \begin{bmatrix} a_{11} & a_{12} & \ldots & a_{1n}\\\\a_{21} & a_{22} & \ldots & a_{2n}\\\\ \vdots & \vdots & \ldots & \vdots\\\\a_{m1} & a_{m2} & \ldots & a_{mn}\end{bmatrix}\]

VSM中的三个关键问题：

• 词项的选择：选择什么样的单位作为向量的每一维(特征、词项粒度、降维)
• 权重计算：即计算每篇文档中每个词项的权重，即得到向量的每一维大小(TF、IDF)
• 相似度计算：计算向量之间的相似度(内积、夹角)

1.3.2 信息论

信息论即香农(Claude Edwood Shannon, 1916-2001 )信息论，也称经典信息论，是研究通信系统极限性能的理论。

信息论是研究信息的基本性质及度量方法，研究信息的取得、传输、存贮、处理和变换的一般规律的科学。

1948年，美国工程师和数学家香农 (Claude Edwood Shannon, 1916-2001 )发表了《通信的数学理论》（A Mathematical Theory of Communication，BSTJ，1948）标志着信息论的产生。

熵

一个离散随机变量X，其概率分布函数为p(x)，则X的熵定义为:

\[H(X) = -\sum_xp(x)log\,p(x) = \sum_xp(x)log\,\frac{1}{p(x)}\]

通常对数以2为底， H代表了X的信息量，也可以认为是对X进行二进制编码所需要的平均编码长度：

\[0\le H(x)\le log\,|X|\]

• X只取某个确定值的时左边等号成立
• X为均匀分布时右边等号成立

也就是说：一个变量的不确定性越大，熵也就越大，把它搞清楚所需要的信息量也就越大

联合熵

随机变量X、Y的联合分布是p(x,y)，它们的联合熵(Joint Entropy)为：

\[H(X,Y)=-\sum_x\sum_y p(x,y)log\,p(x,y)=\sum_x\sum_y p(x,y)\frac{1}{log\,p(x,y)}\]

条件熵

条件熵(Conditional Entropy)(给出另外一个随机变量后，当前随机变量的信息熵还有多少)

\[H(X|Y)=-\sum_x\sum_y p(x,y)log\,p(x|y)=\sum_x\sum_y p(x,y)\frac{1}{log\,p(x|y)}\]

互信息

互信息(Mutual Information)(是变量之间相互依赖的度量)

\[I(X,Y)=H(X)-H(X|Y)=\sum_x\sum_y p(x,y)log\,\frac{p(x,y)}{p(x)p(y)}\]

如果互信息越大，说明X变量对Y变量的依赖程度就越强，也就是说：当Y的信息给出之后，我们对X的了解就会足够多了

---

---

2 机器学习常用技术之分类

分类的发展

手工方法- –> *(人工撰写)规则的方法- –> *统计概率的方法

Web发展的初期，Yahoo是使用人工分类的方法来组织Yahoo目录的 Google Alerts的例子是基于规则分类的，通常情况下都是一些Boolean表达式的组合 文本分类是一种监督学习的分类，基于统计概率的方法

2.1 文本分类

文本分类的分类流程：

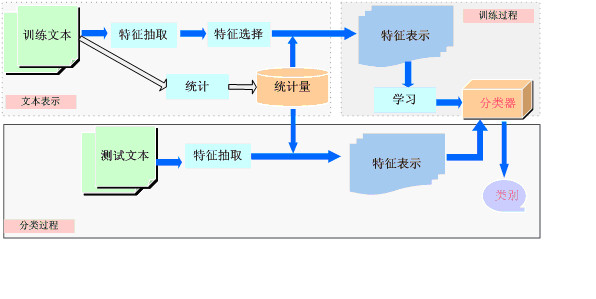
特征选择

• 文本分类中，通常要将文本表示在一个高维空间下，每一维对应一个词项
• 许多维上对应的词(如某些罕见词)对分类作用不大，有时可能会误导分类器，这些特征称为噪音特征（noise feature）
• 去掉这些噪音特征会同时提高文本分类的效率和效果，该过程称为特征选择（feature selection）

特征选择所考虑的因素

• 类内代表性：该特征应该是类别当中的典型特征
  • 偶尔出现一两次的特征不是好特征
• 类间区别性：该特征在多个类别当中具有去分析那个
  • 每个类中都频繁出现的特征不是好特征

不同的特征选择方法

特征的选择方法主要是基于所要使用的特征效用(Utility)指标定义，即定义特征对于分类的有用程度

• 常用的特征效用指标
  • 频率法(DF)-选择高频词汇
  • 信息增益(IG-information gain)
  • 卡方(Chi-square)

信息增益

信息增益(Information Gain, IG)：该特征为整个分类所能提供的信息量(不考虑任何特征的熵和考虑该特征后的熵的差值)

\[IG(t)=Entropy(S)-Expected Entropy(S_t)=-\sum_{i=1}^M P(c_i)log\,P(c_i)-[P(t)(-\sum_{i=1}^M P(c_i|t)log\,P(c_i|t)) + P(\overline t)(-\sum_{i=1}^M P(c_i|\overline t)log\,P(c_i|\overline t))]\]

在某种情况下期望互信息和信息增益是等价的(IG=MI)

卡方法

\(\chi^2\) 统计量(卡方统计量)：度量两者(词项和类别)独立性的缺乏程度， \(\chi^2\)越大，独立性越小，相关性越大。

特征选择VS特征权重的计算

• 特征选择：给定类别c、词汇表的情况下，通过给每个<c,t>打分，选出得分靠前的特征，这里的分表示t与类别c的紧密程度
• 特征权重：给定文档集合，对每篇文档d中的特征t，给出的t在d中的权重。
• 两者不是一回事。有人在分类中，将两者结合为特征的权重。

特征选择的问题：

• 每个类别选前K个特征，K怎么定？ + 交叉验证法评价必须基于测试数据进行，而且该测试数据是与训练数据完全隔离的 (通常两者样本之间无交集) + 通常画出随K变化分类效果变化的曲线
• 每个类别的特征数目能不能不是固定的 + 可以采用阈值截断法
• 每个类别选出来的特征需不需要合在一起形成全局特征空间

文本分类的评价

评价必须基于测试数据进行，而且该测试数据是与训练数据完全隔离的 (通常两者样本之间无交集)

评价指标：指标：正确率、召回率、 F1值、分类精确率(classification accuracy)等等

正确率(Precision)、召回率(Recall)、精确率(Accuracy)

\[\begin{array} {|l|c|r|} \hline & \text {in the class} & \text {not in the class} \\\\ \hline \text {predicted to be in the class} & \text {true positive(TP)} & \text {false positive(FP)} \\\\ \hline \text {predicted to be not in the class} & \text {false negatives(FN)} & \text {true negatives(TN)} \\\\ \hline \end{array}\]

• 正确率 Precision = TP / (TP + FP)
• 召回率 Recall = TP / (TP + FN)

• 精确率 Accuracy = (TP+TN)/(TP + FP + FN + TN)

• “宁可错杀一千，不可放过一人” –> 偏重召回率，忽视正确率。冤杀太多

• 判断是否有罪： + 如果没有证据证明你无罪，那么判定你有罪。–> 召回率高，有些人受冤枉 + 如果没有证据证明你有罪，那么判定你无罪。–> 召回率低，有些人逍遥法外

• 虽然正确率和召回率都很重要，但是不同的应用、不用的用户可能会对两者的要求不一样。因此，实际应用中应该考虑这点。 + 垃圾邮件过滤：宁愿漏掉一些垃圾邮件，但是尽量少将正常邮件判定成垃圾邮件。即尽量减少误判率，提高正确率。 + 特定疾病检测：宁愿误判一些健康人，也不漏掉一个病人。即尽量降低漏判率，提高召回率。

F值

F是R和P的调和平均数，在正确率和召回率之间达到某种平衡

\[\frac{1}{F}=\frac{1}{2}(\frac{1}{P}\,+\frac{1}{R})\]

其他的评价方法还有：混淆矩阵、ROC曲线

训练集合测试集

• 给定一个已标注好的数据集，将其中一部分划为训练集(training set)，另一部分划为测试集(test set)。在训练集上训练，训练得到的分类器用于测试集，计算测试集上的评价指标。
• 另一种做法：将上述整个数据集划分成k份，然后以其中k-1份为训练集训练出一个分类器，并用于另一份(测试集)，循环k次，将k次得到的评价指标进行平均。这种做法称为k折交叉验证(k-cross validation)。如果k=数据集的大小，则称留一法(leave-one-out)。
• 有时，分类器的参数需要优化。此时，可以仍然将整个数据集划分成训练集和测试集，然后将训练集分成k份(其中k-1份作为训练，另一份称为验证集validation set，也叫开发集)，在训练集合上进行k折交叉验证，得到最优参数，然后将得到参数后的分类器应用于测试集。

微平均和宏平均

上面对于一个类得到评价指标P、R、F1，但是我们希望得到分类器在所有类别上的综合性能

• 宏平均(Macro-averaging)：以类为单位
  • 对类别集合C 中的每个类都计算一个P、R、F1值

  • 对

    C

    个结果求算术平均

• 微平均(Micro-averaging): 以类别-文档为单位
  • 对类别集合C 中的每个类都计算TP、FP和FN
  • 将C中的这些数字累加
  • 基于累加的TP、FP、FN计算P、R和F1

2.2 朴素贝叶斯(Naive Bayes)分类器

朴素贝叶斯是一个概率分类器

就文本分类而言，文档d术语类别c的概率计算公式：

\[P(c|d)=\frac{P(d|c)}{P(c)}\,\propto\,P(d|c)P(c)=P(c)\prod_{1\le k \le n_d} P(t_k|c)\]

\(n_d\)是文档的长度(词的个数)

P(c)是类别c的先验概率

\(P(t_k

c)\)是词项\(t_k\)出现在类别c中文档的概率，度量的是类比c中\(t_k\)的贡献

上式的假设是独立性假设

如果文档的词项无法提供属于哪一个类的信息，我们直接选择P(c)最高的那个类

朴素贝叶斯的原理

• 朴素贝叶斯的分类的目标是寻找最佳的类别；朴素贝叶斯之所以称之为朴素，它的原理很简单
• 最佳的类别指的是具有最大后验概率(maximum a posterior-MAP)的类别\(c_{map}\):

\[c_{map}=arg\max_{c \in C}\hat P(c|d)=arg\max_{c \in C}\hat P(c) \prod_{1 \le k \le n_d} \hat P(t_k|c)\]

由于很多小的概率乘积会导致浮点数下溢出且log是单调函数，一次在实际中常常使用的公式是：

\[c_{map}=arg\max_{c \in C}[log \hat P(c) + \sum_{1 \le k \le n_d} log \hat P(t_k|c)]\]

分类的规则：选择后验概率最大的，也就是最有可能的那个类别

朴素贝叶斯的实现方式

1. 多项式模型的实现方式
2. 伯努利模型的实现方式
3. 高斯朴素贝叶斯(基于正太分布，用于处理连续型特征)

多项式模型朴素贝叶斯

基于多项式模型的实现方法：多项式模型中各单词类条件概率计算考虑了词出现的次数，多项式模型是一种以词作为计算粒度的方法。

• 多项式模型认为：每个类的一篇文档是上帝掷骰子的结果
  • 每一个不同的规则筛子代表一个类 + 筛子的每一个面代表一个词 + 筛子面的个数等于文本中单词的个数

多项式朴素贝叶斯的参数估计也是以上面的假设为前提的

先验概率的估计：

\[\hat P(c)=\frac {N_c}{N}\]

\(N_c\)表示类c中文档数目；N表示所有的文档总数

条件概率估计：

\[\hat P(t|c)=\frac {T_{ct}}{\sum_{t' \in V}T_{ct'}}\]

• \(T_{ct}\)是训练集中类别c中词条t的个数(多次出现要计算多次)，V代表整个词汇表，是不同词语的个数
• 位置独立性假设(positional independence assumption)：\(\hat P(t_{k_1})=\hat P(t_{k_2})\)

伯努利模型朴素贝叶斯

基于伯努利模型的实现方法：伯努利模型中各单词类条件概率计算考虑了词所在的文档占整个文档的比例，多项式模型是一种以词作为计算粒度的方法。伯努利模型认为文档中单词出现一次与出现多次等效，只有出现与不出现的区别。

• 基于贝努利模型的实现方法：贝努利模型不考虑词在文档中出现的次数，只考虑出不出现，因此在这个意义上相当于假设词是等权重的。贝努利模型是一种以文档作为计算粒度的方法。 + 每个类对应一堆硬币 + 每一个硬币代表一个词 + 硬币的个数等于单词的个数 + 类中的一篇文本是通过投掷对应类的所有硬币产生的

高斯朴素贝叶斯

高斯朴素贝叶斯用来处理连续型值的特征，可以用高斯模型求解：

\[P(x_i|w_i)=\frac {1}{\sqrt{2\pi\sigma_{w_i}^2}}exp\{-\frac{(x_i - \mu_{w_i})^2}{2\sigma_{w_i}^2}\}\]

其中，均值、方差可以利用MLE估计求解

0概率处理-加一平滑法

参数估计的时候，有可能遇到0概率的事件，这时候就必须将0概率处理掉，防止结果出现0的情况

一般次用加一平滑的方法进行处理，以多项式贝叶斯为例子进行说明：

• 平滑前：

\[\hat P(t|c)=\frac {T_{ct}}{\sum_{t' \in V}T_{ct'}}\]

• 平滑后：

\[\hat P(t|c)=\frac {T_{ct}+1}{\sum_{t' \in V}T_{ct'}+1}=\frac {T_{ct}+1}{(\sum_{t' \in V}T_{ct'})+B}\]

B的个数就是整个单词表的个数

朴素贝叶斯特点：

• 朴素贝叶斯的假设有两个：条件独立性假设和位置独立性假设
• 相对于其他很多更复杂的学习方法，朴素贝叶斯对不相关特征更具鲁棒性
• 相对于其他很多更复杂的学习方法，朴素贝叶斯对概念漂移(concept drift)更鲁棒(概念漂移是指类别的定义随时间变化)
• 当有很多同等重要的特征时，该方法优于决策树类方法
• 一个很好的文本分类基准方法 (当然，不是最优的方法)
• 如果满足独立性假设，那么朴素贝叶斯是最优的 (文本当中并不成立，但是对某些领域可能成立)
• (训练和测试)速度非常快
• 存储开销少
• 朴素贝叶斯起作用的原因：准确估计 –> 精确预测，分类的目标是预测正确的类别，并不是准确的估计概率

2.3 中心向量分类器

中心向量分类器思想

• 计算每个类的中心向量：

\[\vec{u}(c)=\frac{1}{|D_c|}\sum_{d \in D_c}\vec{v}(d)\]

其中，\(D_c\)是所有属于类别c的文档，\(\vec{v}(d)\)是文档d的向量空间表示

• 将每一篇测试文档分到离它最近的那个中心向量

中心向量的性质：

• 简单地将每个类别表示成其中心向量
• 中心向量可以看成类别的原型或代表(prototype)
• 分类基于文档向量到原型的相似度或距离来进行
• 并不保证分类结果与训练集一致，即得到分类器后，不能保证训练集中的文档能否正确分类

很多情况下，中心向量法的效果不如朴素贝叶斯。一个原因是，中心向量法不能正确处理非凸、多模式类别问题

2.4 KNN分类器

KNN，K Nearest Neighbor分类器。

KNN分类器思想

• KNN分类的基本原理是：邻近性假设-我们期望一篇测试文档d与训练集中d周围邻域文档的类别标签一样。
• k = 1 情况下的kNN (最近邻): 将每篇测试文档分给训练集中离它最近的那篇文档所属的类别。
  • 1NN 不很鲁棒—一篇文档可能会分错类或者这篇文档本身就很反常
• k > 1 情况下的kNN: 将每篇测试文档分到训练集中离它最近的k篇文档所属类别中最多的那个类别

KNN讨论

• 优点
  • 不需要训练过程
  • 文档的线性预处理过程和朴素贝叶斯的训练开销相当
  • 对于训练集来说我们一般都要进行预处理，因此现实当中kNN的训练时间是线性的。
  • 当训练集非常大的时候，kNN分类的精度很高
• 缺点
  • 如果训练集很小， kNN可能效果很差。
  • 需要确定参数k (可以采用多折交叉验证法)
  • kNN倾向于大类，可以将相似度考虑在内：

\[score(c,d)=\sum_{d' \in S_k}I_c(d')\cos(\vec v(d'),\vec v(d))\]

KNN的一种快速实现方式是：KD-树

2.5 线性分类器

所谓的线性二类分类器是：存在一条线或者一个超平面能偶将两个类别分离开来。

• 线性分类器：\(\sum_i w_i x_i\)
• 训练所有的\(w_i\)和参数\(\theta\)
• 决策规则：\(\sum_i w_i x_i \gt \theta\)
• 对于线性可分，必然存在线性分类平面：\(\sum_i w_i x_i = \theta\)

中心向量分类器是一个线性分类器 朴素贝叶斯分类器也是一个线性分类器 KNN分类器不是一个线性分类器

2.6 感知机

基本概念

• 感知机(perceptron)是1957年由Rosenblatt提出，是神经网络和支持向量机的基础
• 感知机，是二类分类的线性分类模型，其输入为样本的特征向量，输出为样本的类别，取+1和‐1二值，即通过某样本的特征，就可以准确判断该样本属于哪一类。感知机能够解决的问题首先要求特征空间是线性可分的，再者是二类分类，即将样本分为{+1, ‐1}两类。由输入空间到输出空间的符号函数：

\[f(x)=sign(w\cdot x + b)\]

w和b是感知机参数，分别代表权重和偏置(bias)

模型-Sign函数

\[sign(w\cdot x + b) = \begin{cases}+1&\mbox w\cdot x + b \ge 0 \\\\ -1&\mbox w\cdot x + b \lt 0 \end{cases}\]

策略-损失函数最小化

损失函数是：误分点到超平面\(S(w\cdot x + b = 0)\)的距离和。

误分点\((x_i,y_i)\)到超平面S的距离为：

\[-\frac{y_i(w\cdot x_i + b)}{||w||}\]

假设误分点的集合是M，则所有误分点到超平面S的距离和为：

\[-\frac{\sum_{x_i \in M}y_i(w\cdot x_i + b)}{||w||}\]

由于w的值是固定的，我们就可以得到损失函数：

\[\min_{w,b}L(w,b)=-\sum_{x_i \in M}y_i(w\cdot x_i + b)\]

算法-梯度下降法

感知机算法的原始形式：\(\min_{w,b}L(w,b)=-\sum_{x_i \in M}y_i(w\cdot x_i + b)\)

• 我们使用梯度下降法来记性求解，损失函数的梯度为：

\[\nabla_w L(w,b)=-\sum_{x_i \in M}y_i x_i\] \[\nabla_b L(w,b)=-\sum_{x_i \in M}y_i\]

• 随机选取的一个误分点\(x_i,y_i\)对w,b进行更新

\[w+\eta y_i x_i \to w\] \[b+\eta y_i \to b\]

其中，\(\eta(0 \lt \eta \lt 1)\)为步长，也称为学习速率，一般在0到1之间取值，通过迭代，直到损失函数为0

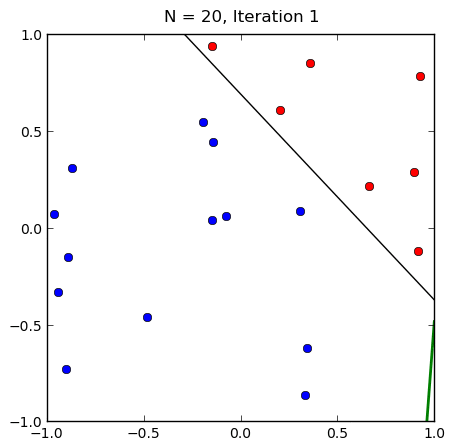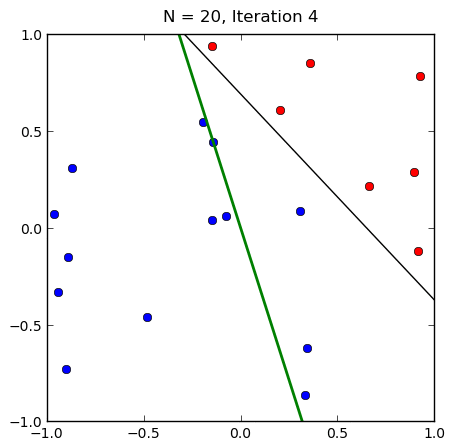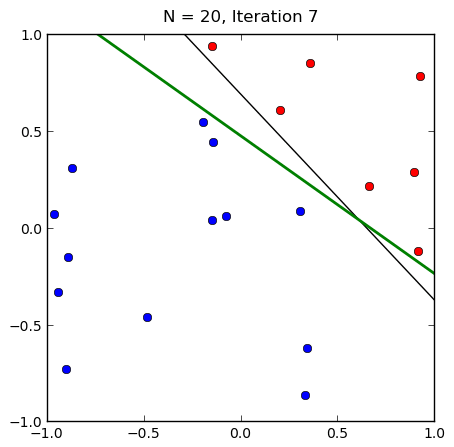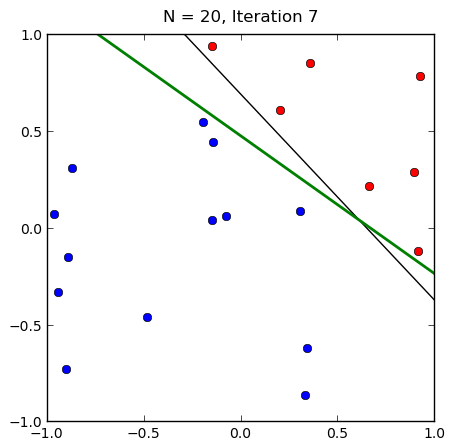
感知机的收敛性

• 在线性可分的情况下，可以证明感知机一定收敛(学习率要足够小)
• 取任意初值，感知机都会收敛，但是不同初值，最后得到的超平面不一定相同
• 线性不可分的情况下，感知机不收敛，一般迭代到一定次数或者达到某个预定情形迭代结束，或者采用梯度下降策略。

2.7 支持向量机

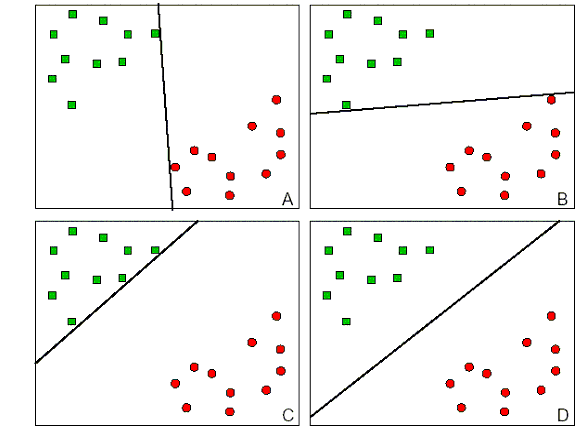
研究起因

• 如何找到最优的超平面
  • 直观上最有效
  • 概率的角度，就是使得置信度最小的点置信度最大
  • 即使我们在选边界的时候犯了小错误，使得边界有偏移，仍然有很大概率保证可以正确分类绝大多数样本
  • 很容易实现交叉验证，因为边界只与极少数的样本点有关
  • 有一定的理论支撑(如VC维)
  • 实验结果验证了其有效性

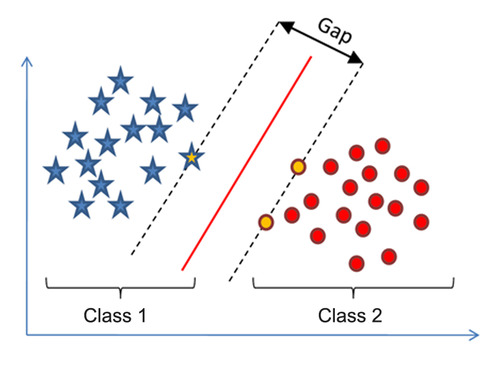
支持向量机思想

找到一个最优超平面。最优超平面是指两类的分类间隔(Margin)最大，即每类距离超平面最近的样本到超平面的距离之和最大。距离这个最优超平面最近的样本被称为支持向量(Support Vector)。

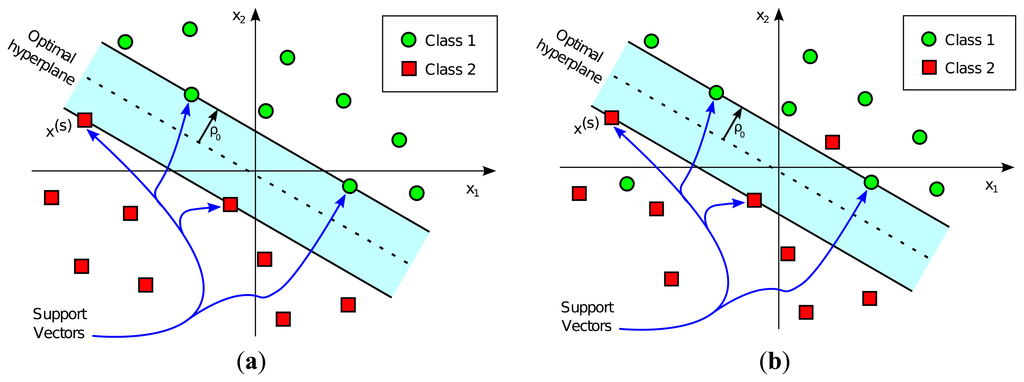
2.7.1 线性可分支持向量机

策略

• 给定训练数据\(x_i \in {X=R^n}\)，其类标签为\(y_i \in {Y=\{+1,-1\}}\)
• 点\(x_i\)到平面\(w\cdot x + b = 0\)的距离：

\[\gamma_i=\frac{y_i(w\cdot x_i + b)}{||w||}\]

• 切分面满足距离：

\[\gamma=\min_{i=1,\cdots,N}\frac{y_i(w\cdot x_i + b)}{||w||}\]

• 转化为优化问题：

\[obj\qquad\max_{w,b}\gamma\] \[s.t.\qquad \frac{y_i(w\cdot x_i + b)}{||w||} \ge \gamma,i=1,\cdots,N\]

因为若将w和b按比例改变为λw和λb，则函数间隔变为λr，而超平面没有发生改变。说明上述的最优化目标函数不足以代表最近的点到超平面的距离

• 引入函数间隔\(\hat \gamma\)：

\[\gamma = \frac{\hat \gamma}{||w||}\]

• 间隔转换：

\[obj\qquad\max_{w,b}\frac{\hat \gamma}{||w||}\] \[s.t.\qquad y_i(w\cdot x_i + b) \ge \hat \gamma,i=1,\cdots,N\]

• 令\(\hat \gamma=1\)，进一步转化：

\[obj\qquad\max_{w,b}\frac{1}{||w||}\] \[s.t.\qquad y_i(w\cdot x_i + b) \ge 1,i=1,\cdots,N\]

• 等价于：

\[obj\qquad\min_{w,b}\frac{1}{2}||w||^2\] \[s.t.\qquad y_i(w\cdot x_i + b) \ge 1,i=1,\cdots,N\]

算法

上述最优化问题是带有线性约束的二次规划问题，利用拉格朗日对偶进行求解

• 拉格朗日算子：

\[\min_{w,b}\qquad L(w,b,\alpha_i) = \frac{1}{2}||w||^2-\sum_{i=1}^N\alpha_i(y_i(w\cdot x_i + b) -1)\] \[s.t.\qquad \alpha_i \ge 0\]

理解上述转化过程：用惩罚项来表达限制条件，从而能够转化带限制的优化问题为无限制的优化问题

\[\min_{w,b}\frac{1}{2}||w||^2 + \text{penality term}\]

为训练中的每一个数据样本，定义penality term：

\[\begin{Bmatrix} 0 & y_i(w\cdot x_i+b)\ge 1 \\\\ \infty & otherwise \end{Bmatrix}=max_{\alpha_i \ge 0}\alpha_i(y_i(w\cdot x_i + b) -1)\]

将问题转化为：

\[\min_{w,b}\{\frac{1}{2}||w||^2-\sum_{i=1}^N\max_{\alpha_i \ge 0}\alpha_i(y_i(w\cdot x_i + b) -1)\}\] \[\Updownarrow\] \[\min_{w,b}\qquad L(w,b,\alpha_i) = \frac{1}{2}||w||^2-\sum_{i=1}^N\alpha_i(y_i(w\cdot x_i + b) -1)\] \[s.t.\qquad \alpha_i \ge 0\]

• 求解最优化问题

\[\frac{\partial L}{\partial w}=0 \Longrightarrow w=\sum_{i=1}^N\alpha_i y_i x_i\] \[\frac{\partial L}{\partial b}=0 \Longrightarrow \sum_{i=1}^N\alpha_i y_i=0\]

• 转化为对偶问题：

\[\min_{w,b}\{\frac{1}{2}||w||^2-\sum_{i=1}^N\max_{\alpha_i \ge 0}\alpha_i(y_i(w\cdot x_i + b) -1)\}\] \[\Updownarrow\] \[\min_{w,b}\max_{\alpha_i \ge 0}\{\frac{1}{2}||w||^2-\sum_{i=1}^N\alpha_i(y_i(w\cdot x_i + b) -1)\}\] \[\Updownarrow\] \[\max_{\alpha_i \ge 0}\min_{w,b}\{\frac{1}{2}||w||^2-\sum_{i=1}^N\alpha_i(y_i(w\cdot x_i + b) -1)\}\] \[\Updownarrow \sum_{i=1}^N\alpha_i y_i=0\] \[obj\qquad\max_{\alpha_i \ge 0}\min_{w,b}\{\sum_{i=1}^N\alpha_i-\frac{1}{2}\sum_i^N\sum_j^N\alpha_i\alpha_jy_iy_j(x_i\cdot x_j)\}\] \[s.t.\qquad \sum_{i=1}^N\alpha_i y_i=0\] \[\Updownarrow\] \[obj\qquad\min_{w,b,\alpha_i \ge 0}\{\frac{1}{2}\sum_i^N\sum_j^N\alpha_i\alpha_jy_iy_j(x_i\cdot x_j) - \sum_{i=1}^N\alpha_i\}\] \[s.t.\qquad \sum_{i=1}^N\alpha_i y_i=0\]

由于是凸二次规划且满足Slater条件，故原问题满足强对偶性，能够求得\(\alpha^*=(\alpha_1^*,\alpha_2^*,\cdots,\alpha_n*)\)满足KKT条件：

\[\alpha_j^*(y_j^*(w_j^*\cdot x_j + b^*)-1)=0\]

• 求出结果：

\[w^*=\sum_{i=1}^N\alpha_i^*y_ix_i\]

\[b^*=y_j-\sum_{i=1}^N\alpha_i^*y_i(x_i\cdot x_j)\]

支持向量和分类：

\[f(x)=sign(w^*\cdot x + b^*)=\left\{ {+1 \atop -1} \right. \]

2.7.2 线性支持向量机

线性可分支持向量机存在的问题：

• 硬间隔最大化
  • 无训练错误
• 训练集中如果有噪声
  • 硬间隔的分类容易受到少数点的控制，很危险-造成过拟合(Overfitting)

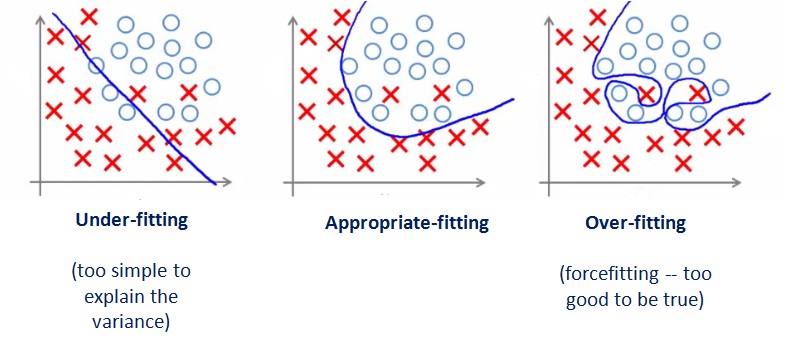
线性支持向量机思想

• 仿照人的思路，允许一些点到分类平面的距离不满足原先的硬间隔要求

• 寻找最小的\(

  w

  ^2\)，同时使错分的样本到超平面的距离最短

\[\min||w||^2+c(\text{error distances})\]

策略：

\[obj\qquad\min_{w,b}\frac{1}{2}||w||^2 + C\sum_{i=1}^N\xi_i\] \[s.t.\qquad y_i(w\cdot x_i + b) \ge 1-\xi_i,\] \[\xi_i \ge 0,i=1,\cdots\,N\]

算法：

拉格朗日对偶化：

\[obj\qquad\max\{\sum_{i=1}^N\alpha_i-\frac{1}{2}\sum_i^N\sum_j^N\alpha_i\alpha_j y_i y_j(x_i\cdot x_j)\}\] \[s.t.\qquad 0 \le \alpha_i \le C,i=1,2,\cdots,N\] \[\sum_{i=1}^N\alpha_i y_i = 0\]

推导过程同线性可分支持向量机推导过程类似

求解：

\[w^*=\sum_{i=1}^N\alpha_i^*y_ix_i\]

\[b^*=y_j(1-\xi_j)-\sum_{i=1}^N\alpha_i^*y_i(x_i\cdot x_j)\]

\[\text{where}\quad j=\max_{j’}\alpha_{j’}^*\]

这里的b解不唯一，能求出来一组值，我们一般去最大的α对应的支持向量来计算b的值

使用SVM进行分类：

• 硬间隔进行分类：

\[f(x)=sign(w^*\cdot x + b^*)=\left\{ {+1 \atop -1} \right. \]

• 设定置信度阈值t
  • Score > t，正类
  • Score < t，负类
  • Else，无法判断

软间隔的支持向量

软间隔支持向量或者在间隔边界上，或者在间隔边界与分离超平面之间，或者在分离超平面误分的一侧

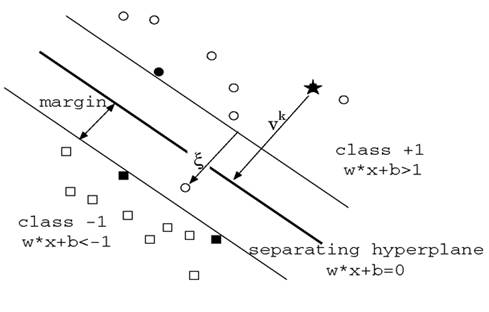
参照推导：

\[\Delta_\xi L(w^*,b^*,\xi^*,\alpha^*,\mu^*) = C - \alpha^- - \mu^- = 0\]

\[\alpha^*(y_i(w^*\cdot x_i + b^*)-1+\xi^*)=0\]

\[\mu_i^- \xi_i^- = 0\]

线性支持向量机总结：

• 分类器是一个超平面\(w\cdot x + b = 0\)
• “支持向量们”是最重要的训练样本，决定超平面的位置
• 通过发现对应的α是否为0，二次规化算法可以发现哪些点是“支持向量”
• 在问题的对偶形式及其解中，训练样本之间的关系都是线性的（内积）(这一点在引入核函数相当重要)

2.7.3 非线性支持向量机

非线性支持向量机的基本思想：

将原始数据向高位特征空间映射，使得数据在新的空间内线性可分。

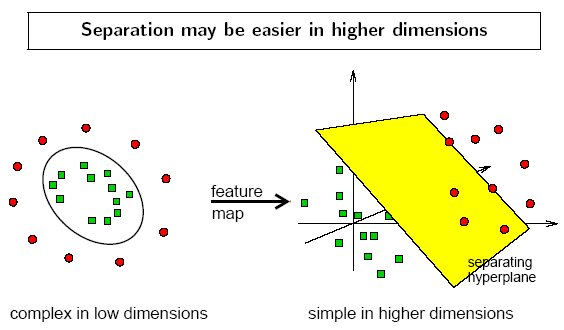
核函数(Kernel function)

• 最初想解决线性不可分问题的思路是向高维空间转化，使其变得线性可分。而转化最关键的部分就在于找到映射方法。可是，如何找到这个映射，没有系统性的方法。而且高维空间和映射函数也并不是唯一的，过于复杂，并且会导致维度灾难！

事实上，上面的例子不能够用一条直线(超平面)将之分开，也就是线性不可分的，但是我们可以发现：用一条二次曲线能偶将之分开(例如，椭圆)。如果用\(X_1\)和\(X_2\)表示二维平面的两个坐标的话，我们知道一条二次曲线的方程可以写成下面的形式：

\[a_1 X_1 + a_2 X_1^2 + a_3 X_2 + a_4 X_2^2 + a_5 X_1 X_2 + a_6\]

我们可以将原来的二维空间转化为五维空间，其中的五个维度的坐标值分别为：\(Z_1=X_1,Z_2=X_1^2,Z_3=X_2,Z_4=X_2^2,Z_5=X_1 X_2\)，那么显然上面的方程式就可以写成：

\[\sum_{i=1}^5 a_i Z_i + a_6 = 0\]

那么，上述五维空间的方程，正是一个超平面。也就是说，我么做了一个映射：\(\phi:R^2 \rightarrow R^5\)，将X按照上面的规则映射为Z，那么在新的数据空间中原来的数据就变得线性可分了，从而可以使用线性可分支持向量机计算超平面了。这是Kernel处理非线性问题的核心思想。

核函数将原来的分类函数：

\[f(x)=\sum_{i=1}^N\alpha_i y_i \langle x_i,x \rangle + b\]

映射为：

\[f(x)=\sum_{i=1}^N \alpha_i y_i \langle \phi(x_i),\phi(x) \rangle + b\]

而α可以通过对偶问题求解：

\[obj\qquad\max\{\sum_{i=1}^N\alpha_i-\frac{1}{2}\sum_i^N\sum_j^N\alpha_i\alpha_j y_i y_j \langle \phi(x_i) , \phi(x_j) \rangle\}\] \[s.t.\qquad \alpha_i \ge 0,i=1,2\cdots,N\] \[\sum_{i=1}^N\alpha_i y_i = 0\]

这样一来，似乎问题就解决了，我们可以通过将向量空间中的向量全部映射到高维特征空间即可。但是，如果向量空间特征向量的维度是3，那么需要映射到19维的空间中，计算的复杂度大大增加了，如果遇到无穷的情况，根本无法计算。这个时候就使用到了”核函数”。

• 在线性SVM中的对偶形式中，目标函数和分离超平面都只需要计算内积，只关心计算那个高维空间里内积的值。不必显式的给出映射函数和值。

考虑面一个简单的例子：设两个向量\(x_1=(\eta_1,\eta_2)^T\)和\(x_1=(\xi_1,\xi_2)^T\)，映射函数\(\phi(\cdot)\)是前面所说的五维空间的映射，因此映射后的内积为

\[\langle\phi(x_1),\phi(x_2)\rangle=\eta_1\xi_1 + \eta_1^2\xi_1^2 + \eta_2\xi_2 + \eta_2^2\xi_2^2 + \eta_1\eta_2\xi_1\xi_2\]

同时：

\[(\langle x_1,x_2 + 1\rangle)^2=2\eta_1\xi_1 + \eta_1^2\xi_1^2 + 2\eta_2\xi_2 + \eta_2^2\xi_2^2 + 2\eta_1\eta_2\xi_1\xi_2 + 1\]

实际上，上述的两个式子，只要做稍微的调整就会相等，也就是说，我们可以原来空间中的函数来进行替代高维特征空间映射函数的内积运算。

我们称这里计算两个向量在隐式映射后的内积的函数就做核函数(Kernel Function)

例如，刚才的核函数为：

\[k(x_1,x_2)=(\langle x_1,x_2\rangle+1)^2\]

核函数能够简化映射空间中内积的运算。而我们SVM中要计算的地方，数据总是以内积的形式出现，那么高维空间的分类函数就可以写成：

\[f(x)=\sum_{i=1}^N \alpha_i y_i k(x_i,x) + b\]

其中的α由对偶问题求得：

\[obj\qquad\max\{\sum_{i=1}^N\alpha_i-\frac{1}{2}\sum_i^N\sum_j^N\alpha_i\alpha_j y_i y_j k(x_i,x_j)\}\] \[s.t.\qquad \alpha_i \ge 0,i=1,2\cdots,N\] \[\sum_{i=1}^N\alpha_i y_i = 0\]

核函数的选择

• Mercer定理：判断核函数的有效性

\[K_{ij}=K(x_i,x_j)\]

重要条件是核函数矩阵K是半正定的，这样的核函数是有效的核函数。

• 常用核函数

  • 高斯(一种径向基(RBF)函数)核：\(K(x_i,x_j)=exp(-

    x_i-x_j

    ^2)/2\sigma^2\)。这个核就是将原始空间映射为无穷维空间的那个家伙。不过，如果选得很大的话，高次特征上的权重实际上衰减得非常快，所以实际上（数值上近似一下）相当于一个低维的子空间；反过来，如果选得很小，则可以将任意的数据映射为线性可分——当然，这并不一定是好事，因为随之而来的可能是非常严重的过拟合问题。不过，总的来说，通过调控参数，高斯核实际上具有相当高的灵活性，也是使用最广泛的核函数之一。

  • 多项式核：\(K(x_i,x_j)=(R+x_i\cdot x_j)^D\)
  • 线性核：\(K(x_i,x_j)=(x_i\cdot\ x_j)^2\)

非线性支持向量机的流程：

• 选择一个核函数K（用以计算样本内积）
• 选择一个C值(参数，控制软间隔程度以及防止过拟合)
• 利用训练样本，求解二次规划问题(可以使用大量软件包)
• 根据支持向量与切分面构造切分函数sign(.)
• 根据切分函数，对测试样本进行分类

序列最小最优化算法(SMO)

参考论文：《Sequential Minimal Optimization A Fast Algorithm for Training Support Vector Machines》

支持向量机总结：

• 优点
  • 有坚实理论基础的新颖的小样本学习方法
  • 平均而言，在各类应用中表现最佳
  • 结果稳定、可重复，且不依赖于特定的优化算法、数据
  • 使用凸优化可以得到全局解，且使用2范数防止过拟合
• 缺点
  • 需要调节参数
  • 核函数高维映射使得结果有时难以直观理解
  • 有一定的计算复杂度

2.8 其他分类方法

2.8.1 决策树方法

决策树方法思想：

将文本的特征进行优先度排序，并将每次的特征作为判定条件(子树的根节点)进行扩展，最后生成一颗树。

常用的构造决策树的构造器：

• 使用某个函数(如IG)来判断特征优先级
  • CART
  • C4.5
  • CHAID
• 决策树剪枝
• 分类：按照决策树的条件进行判定

决策树方法小结：

• 决策树方法是一种规则方法，可以生成可以理解的规则(if… then…)
• 决策树方法会遇到过学习问题(Overfitting)：训练集合的样例都满足得较好，一推广则性能马上下降。
• 效果一般，但是有时很好。

2.8.2 回归方法

回归：用一条直线(线性回归)或者曲线去拟合已有的例子。

LLSF(Linear Least Square Fit) 方法

• \(

  \langle F,A \rangle - B

  \)，A是所有例子构成的矩阵，F是要求的权重矩阵，B是布尔矩阵，1表示属于该类，0表示不属于。

• F求出以后，对新来的文本D，计算结果，哪个最大属于哪个类。

LLSF小结：

• 训练：计算类别权重矩阵F的过程，比较耗时。
• 分类：类别权重矩阵和文档向量相乘。
• Yang Yiming通过实验证实LLSF的效果和kNN、SVM相当。

2.8.3 基于投票的方法(集成方法)

• Bagging方法
  • 训练R个分类器\(f_i\)，分类器之间其他相同就是参数不同。其中fi是通过从训练集合中(N篇文档)随机取(取后放回)N次文档构成的训练集合训练得到的。
  • 对于新文档d，用这R个分类器去分类，得到的最多的那个类别作为d的最终类别
• Boosting方法
  • 类似Bagging方法，但是训练是串行进行的，第k个分类器训练时关注对前k-1分类器中错分的文档，即不是随机取，而是加大取这些文档的概率
  • AdaBoost
  • AdaBoost MH

3 多类下的单标签和多标签问题

通过二类分类器处理多类问题：

• 1-V-R方式：4个类别A、B、C、D，训练A vs BCD、B vs ACD、C vs ABD和D vs ABC四个二类分类器
  • 分类器数目少，N个分类器
  • 但是训练的样本数目大，还可能有非均衡问题
• 1-V-1方式：4个类别A、B、C、D，训练 A vs B, A vs C, A vs D, B vs C, B vs D, C vs D 六个二类分类器
  • 分类器数目多，N(N-1)/2个分类器
  • 但是每个分类器训练的样本数目小
  • LIBSVM采用了这种方式

单标签问题：

• 单标签分类问题，也称single label problem
  • 类别之间互斥
  • 每篇文档属于且仅属于某一个类
  • 例子：文档的语言类型 (假定：任何一篇文档都只包含一种语言)
• 基于线性分类器的单标签分类(多类)
  • 对于单标签分类问题（比如A、B、C三类），可以将多个二类线性分类器(A vs BC、B vs AC、C vs AB)进行如下组合：
    • 对于输入文档，独立运行每个分类器
    • 将分类器排序 (比如按照每个分类器输出的在A、B、C上的得分)
    • 选择具有最高得分的类别
  • 也可以采用1-V-1方式，进行投票

多标签问题：

• 多标签分类问题，也称multi-label problem
  • 一篇文档可以属于0、1或更多个类
  • 针对某个类的决策并不影响其他类别上的决策
  • 一种 “独立”类型，但是不是统计意义上的“独立”
  • 例子：主题分类
  • 通常：地区、主题领域、工业等类别之上的决策是互相独立的
• 基于线性分类器的多标签分类
  • 对于多标签分类问题（比如A、B、C三类），可以将多个二类线性分类器(A vs BC、B vs AC、C vs AB)进行如下组合：
    • 对测试文档独立地运行每个分类器
    • 按照每个分类器自己的输出结果进行独立决策
  • 采用1-V-1方式，也可以使用上述类似思路进行处理

**-

**-

3 聚类问题

聚类是一种常见的无监督学习(Unsuperivesed Learning)方法，无监督意味着没有已经标注好的数据集

文档聚类：将一系列文档按照相似性聚团成子集或者簇(cluster)的过程，簇内文档之间彼此相似；簇间文档之间相似度不大

3.1 聚类的评价

• 内部准则
  • 一个内部准则的例子： K-均值聚类算法的RSS值
  • 内部准则往往不能评价聚类在应用中的实际效用
• 外部准则
  • 按照用户定义的分类结果来评价，即对一个分好类的数据集进行聚类，将聚类结果和事先的类别情况进行比照，得到最后的评价结果

外部准则之纯度：

\[\text{purity}(\Omega,C)=\frac{1}{N}\sum_k\max_j|\omega_k\cap c_j|\]

• \(\Omega={\omega_1,\omega_2,\cdots,\omega_K}\)是簇的集合
• \(C={c_1,c_2,\cdots,c_J}\)是类别的集合
• 对于每一个簇\(\omega_k\)找出一个类别\(c_j\)，该类别包含\(\omega_k\)中的元素最多，为\(n_{ki}\)个，也就是说\(\omega_k\)的元素最多分布在\(c_j\)中
• 将所有的\(n_{ki}\)求和，然后除以所有的文档数目

外部准则之蓝迪系数(Rand Index)：

$$RI=\frac{TP + TN}{TP + FP + FN + TN}

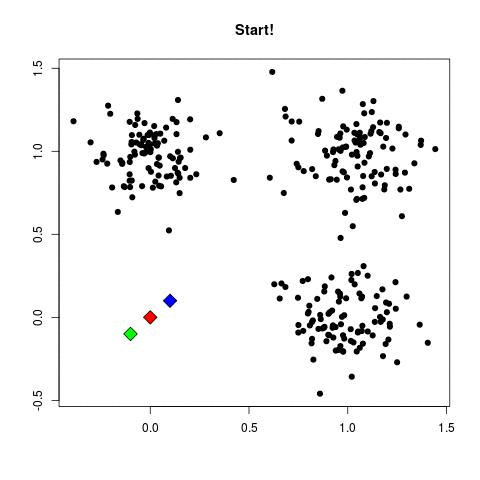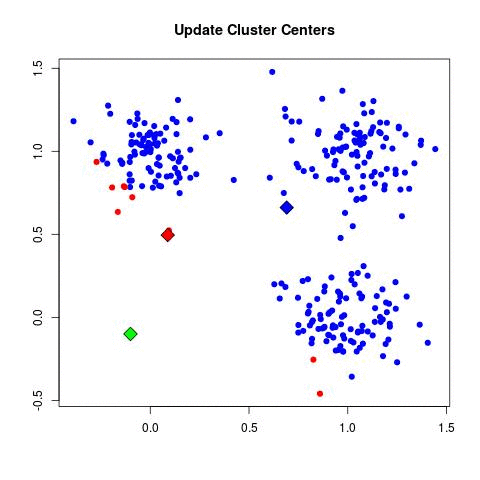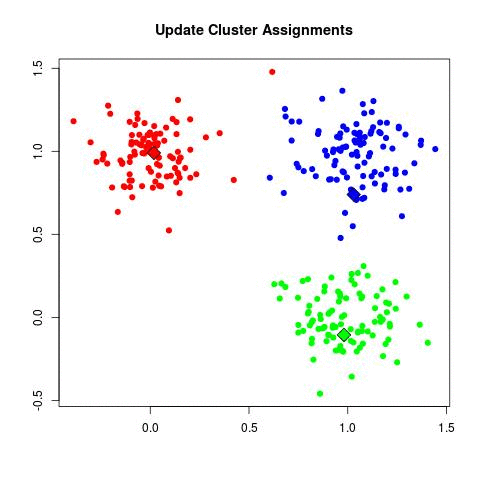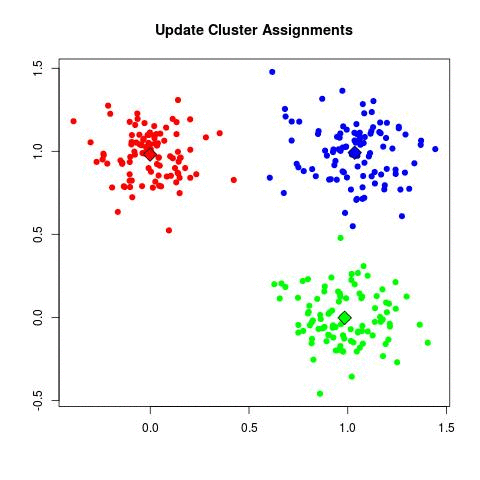
3.2 K-Means聚类算法

• K-均值聚类算法中的每个簇都定义为其质心向量

  • 置心向量的定义：\(\vec \mu(\omega) = \frac{1}{

    \omega

    }\sum_{\vec x \in \omega}\vec x\)，其中\(\omega\)代表一个簇

• 划分准则： 使得所有文档到其所在簇的质心向量的平方和最小
• 通过下列两步来实现目标优化:
  • 重分配(reassignment): 将每篇文档分配给离它最近的簇
  • 重计算(recomputation): 重新计算每个簇的质心向量

K-Means聚类算法的收敛性

• K-Means聚类算法一定是收敛的，但不知道收敛所需要的时间
• 如果不太关心少许文档在不同簇之间来回交叉的话，收敛速度通常会很快 (< 10-20次迭代)
• 完全的收敛需要多得多的迭代过程

K-均值聚类算法的初始化

• 种子的随机选择只是K-均值聚类算法的一种初始化方法之一
• 随机选择不太鲁棒：可能会获得一个次优的聚类结果
• 一些确定初始质心向量的更好办法：
  • 非随机地采用某些启发式方法来选择种子(比如，过滤掉一些离群点，或者寻找具有较好文档空间覆盖度的种子集合)
  • 采用层级聚类算法寻找好的种子
  • 选择 i (比如 i = 10) 次不同的随机种子集合，对每次产生的随机种子集合运行K-均值聚类算法 ，最后选择具有最小RSS值的聚类结果

簇个数的确定

• 在很多应用中，簇个数 K 是事先给定的
• 定义一个优化准则
  • 给定文档，找到达到最优情况的K值
  • 我们不能使用前面所提到的RSS或到质心的平均平方距离等准则，因为它们会导致K = N 个簇

K-means++

• K-means++和传统K-means相比，只有初始中心集合的选择方法不同
  • 首先随机选择一个中心点
  • 然后重复下列计算过程，直到选出k个中心点为止：
    • 计算数据点x到离它最近的中心点的距离d(x)
    • 然后以正比于d(x)的概率将该点加到中心点集合位置

3.3 层次聚类

• 层次聚类算法的目标是生成一个层次结构
• 这个层次结构是自动创建的，可以通过自顶向下或自底向上的方法来实现。最著名的自底向上的方法是层次凝聚式聚类(hierarchical agglomerative clustering，HAC)。

层次凝聚式聚类(HAC)

• HAC会生成一棵二叉树形式的类别层次结构
  • 一开始每篇文档作为一个独立的簇
  • 然后，将其中最相似的两个簇进行合并
  • 重复上一步直至仅剩一个簇
  • 整个合并的历史构成一个二叉树
  • 一个标准的描述层次聚类合并历史的方法是采用树状图(dendrogram)

树状图：

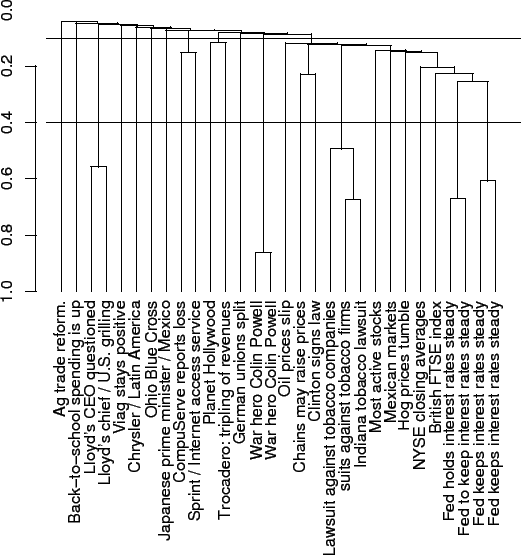
• 合并的历史可以从底往上生成
• 水平线上给出的是每次合并的相似度
• 我们可以在特定点截断 (比如 0.1 或 0.4) 来获得一个扁平的聚类结果

定义簇的相似度

• 单连接(Single-link)：最大相似度
  • 计算任意两篇文档之间的相似度，取其中的最大值
• 全连接(Complete-link): 最小相似度
  • 计算任意两篇文档之间的相似度，取其中的最小值
• 质心法: 平均的类间相似度
  • 所有的簇间文档对之间相似度的平均值 (不包括同一个簇内的文档之间的相似度)
  • 这等价于两个簇质心之间的相似度
• 组平均(Group-average): 平均的类内和类间相似度
  • 所有的簇间文档对之间相似度的平均值 (包括同一个簇内的文档之间的相似度)

3.4 其他的聚类方法

DBSCAN

• DBSCAN (Density-Based Spatial Clustering of Applications with Noise，具有噪声的基于密度的聚类方)算法是一种常见的基于密度的聚类方法
• 大致过程如下：首先把所有的样本标记为核心点、边界点或噪声点。其中一个样本是核心点，满足在该样本的邻域（由距离函数和用户指定的参数R确定）内的样本的个数大于给定的阈值Min。边界点是位于某核心样本邻域的非核心样本，而噪声点指既非核心样本又不是边界样本的样本。然后对每个样本，做如下处理：删除噪声点，而足够靠近的核心点（它们的距离小于R）聚集在同一簇中，与核心点足够靠近（它们的距离小于R）的边界点也聚集在与核心点相同的簇中。
• DBSCAN算法可以有效地发现数据库中任意形状的簇，自动确定聚类的簇个数，但也存在一定的局限性，例如参数R和Min仍然需要用户依靠经验设置。

自组织映射

• 自组织映射(Self Organizing Map, SOM)神经网络是由芬兰神经网络专家Kohonen教授提出的，该算法假设在输入对象中存在一些拓扑结构或顺序，可以实现从输入空间(n维)到输出平面(2维)的降维映射，其映射具有拓扑特征保持性质,与实际的大脑处理有很强的理论联系。
• SOM网络包含输入层和输出层。输入层对应一个高维的输入向量，输出层由一系列组织在2维网格上的有序节点构成，输入节点与输出节点通过权重向量连接。学习过程中，找到与之距离最短的输出层单元，即获胜单元，对其更新。同时，将邻近区域的权值更新，使输出节点保持输入向量的拓扑特征。
• 算法流程：
  • 网络初始化，对输出层每个节点权重赋初值；
  • 将输入样本中随机选取输入向量，找到与输入向量距离最小的权重向量；
  • 定义获胜单元，在获胜单元的邻近区域调整权重使其向输入向量靠拢；
  • 提供新样本、进行训练；
  • 收缩邻域半径、减小学习率、重复，直到小于允许值，输出聚类结果。

谱聚类

• 谱聚类(Spectral Clustering, SC)是一种基于图论的聚类方法——将带权无向图划分为两个或两个以上的最优子图，使子图内部尽量相似，而子图间距离尽量距离较远，以达到常见的聚类的目的。其中的最优指最优目标函数，可以有不同的最优目标函数，比如可以是割边最小分割， 也可以是分割规模差不多且割边最小的分割。

聚类的研究趋势

• 新的聚类算法
• 大规模环境下的聚类算法
• 聚类的评价
• 聚类的应用
  • 事件的发现与跟踪
  • 话题的提取
  • …

---

---

4 回归

回归分析：回归分析是处理变量之间相关关系的一种工具，回归的结果可以用于预测或者分类

线性回归：

• 训练集：m为训练样本的个数，每一个\(x^{(i)}\)是n维向量，\(y^{(i)}\)是一个实数
• 目标-学习函数：

\[h_\theta(x)=\theta_0+\sum_{i=1}^n\theta_i x_i\]

• 代价函数：

\[J(\theta)=\frac{1}{2}\sum_{i=1}^m(h_\theta(x^{(i)})-y^{(i)})^2\]

• 上述方法也称之为：最小二乘法

普通的线性回归的不足

• 缺乏稳定性和可靠性，容易过拟合，有时得到无意义的结果
• 模型可解释性差。很多变量与预测无关，有多个变量同时明显与预测相关，缺乏变量或者说特征选择。
• 一个常用的解决方法：正则化(regularization)，在目标函数上加上正则项(参见SVM的)

岭回归(Ridge Regression)

• 代价函数:

\[J'(\theta)=J(\theta)+\lambda||\theta||_2\]

• 其中θ_2表示向量θ的2范数，即向量的大小
• λ为加权系数

• 特点：
  • 通过加入正则项(惩罚项)，防止过拟合
  • 通过加入2范数正则项，在任何情况下都有解析解，保证了稳定性
  • 解是稠密的，模型可解释性不强

LASSO回归

• LASSO = least absolute shrinkage and selection operator
• 代价函数：

\[J''(\theta)=J(\theta)+\lambda||\theta||_1\]

• 其中θ_1表示向量θ的1范数，即向量的大小
• λ为加权系数

• 特点：
  • 没有解析解，采用迭代求解
  • 解是稀疏的，有特征选择的作用，模型的解释性强

Logistic回归

• Logistic回归是一种非线性回归
• Logistic (也叫Sigmoid)函数(S型曲线)：

\[y=f(x)=\frac{1}{1+e^{-(\alpha + \beta x)}}=\frac{e^{\alpha + \beta x}}{1+e^{\alpha + \beta x}}\]

• Logistic回归可以转化成线性回归来实现

\[\frac{y}{1-y}=e^{\alpha + \beta x},\] \[ln\frac{y}{1-y}=\alpha + \beta x\]

---

---

5 推荐

基于内容的推荐

• 基本思路：基本思路：将与用户C评分很高的物品相似的物品推荐给C
• 电影推荐：
  • 推荐具有相同演员、导演、类型的电影
• 网站博客、博客、新闻：
  • 推荐具有相似内容的网站博客或新闻

基于协同过滤的推荐方法

• 考虑用户c
• 寻找其他用户的一个集合D，这个集合中的用户对物品的评分与c类似
• 基于D中用户对多个物品的评分结果估计c对物品的评分

---

---

参考文章：

1. http://blog.csdn.net/v_july_v/article/details/7624837
2. http://www.duzelong.com/wordpress/201508/archives1491
3. http://home.ustc.edu.cn/~yuedong/courseware/ch7.pdf

---